侯瑞哲的博客

文件及硬盘管理是计算机操作系统的重要组成部分，让微软走上成功之路的正是微软最早推出的个人电脑 PC 操作系统，这个操作系统就叫 DOS，即 Disk Operating System，硬盘操作系统。我们每天使用电脑都离不开硬盘，硬盘既有大小的限制，通常大一点的硬盘也不过几 T，又有速度限制，快一点的硬盘也不过每秒几百 M。

文件是存储在硬盘上的，文件的读写访问速度必然受到硬盘的物理限制，那么如何才能 1 分钟完成一个 100T 大文件的遍历呢？

想要知道这个问题的答案，我们就必须知道文件系统的原理。做软件开发时，必然要经常和文件系统打交道，而文件系统也是一个软件，了解文件系统的设计原理，可以帮助我们更好地使用文件系统，另外设计文件系统时的各种考量，也对我们自己做软件设计有诸多借鉴意义。

让我们先从硬盘的物理结构说起。

硬盘

硬盘是一种可持久保存、多次读写数据的存储介质。硬盘的形式主要两种，一种是机械式硬盘，一种是固态硬盘。

机械式硬盘的结构，主要包含盘片、主轴、次投币，主轴带动盘片高速旋转，当需要读写盘上的数据的时候，磁头臂会移动磁头到盘片所在的磁道上，磁头读取磁道上的数据。读写数据需要移动磁头，这样一个机械的动作，至少需要花费数毫秒的时间，这是机械式硬盘访问延迟的主要原因。

如果一个文件的数据在硬盘上不是连续存储的，比如数据库的B+树文件，那么要读取这个文件，磁头臂就必须来回移动，花费的时间必然很长。如果文件数据是连续存储的，比如日志文件，那么磁头臂就可以较少移动，相比离散存储的同样大小的文件，连续存储的文件的读写速度要快得多。

机械式硬盘的数据就存储在具有磁性特质的盘片上，因此这种硬盘也被称为磁盘，而固态硬盘则没有这种磁性特质的存储介质，也没有电机驱动的机械式结构。

其中主控芯片处理端口输入的指令和数据，然后控制闪存颗粒进行数据读写。由于固态硬盘没有了机械式硬盘的电机驱动磁头臂进行机械式物理移动的环节，而是完全的电子操作，因此固态硬盘的访问速度远快于机械式硬盘。

但是，到目前为止固态硬盘的成本还是明显高于机械式磁盘，因此在生产环境中，最主要的存储介质依然是机械式硬盘。如果一个场景对数据访问速度、存储容量、成本都有较高要求，那么可以采用固态硬盘和机械式硬盘混合部署的方式，即在一台服务器上既有富态硬盘，也有机械式硬盘，以满足不同文件类型的存储需求，比如日志文件存储在机械式硬盘上，而系统文件和随机读写的文件存储在固态硬盘上。

文件系统

作为应用程序开发者，我们不需要直接操作硬盘，而是通过操作系统，以文件的方式对硬盘上的数据进行读写访问。文件系统将硬盘空间以块为单位进行划分，每个文件占据若干个块，然后在通过一个文件控制块FCB记录每个文件占据的硬盘数据块。

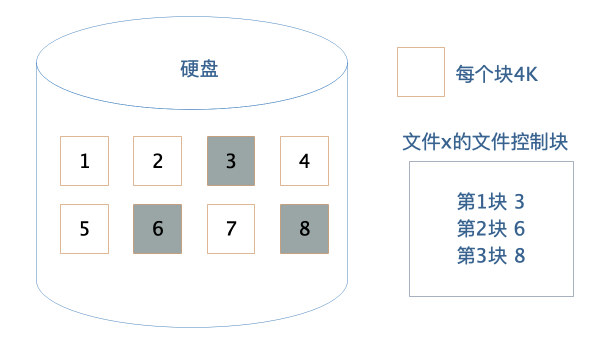
这个文件控制块在Linux操作系统中就是inode，要想访问文件，就必须获得文件的inode信息，在inode中查找文件数据块索引表，根据索引中记录的硬盘地址信息访问硬盘，读写数据。

inode中记录着文件权限、所有者、修改时间和文件大小等文件属性信息，以及文件数据块硬盘地址索引。inode是固定结构的，能够记录的硬盘地址索引数也是固定的，只有15个索引。其中前12个索引直接记录数据块地址，第13个索引记录索引地址，也就是说，索引块指向的硬盘数据块并不直接记录文件数据，而是记录文件数据块的索引表，每个索引表可以记录256个索引；第14个索引记录二级索引地址，第15个索引记录三级索引地址，如下图：

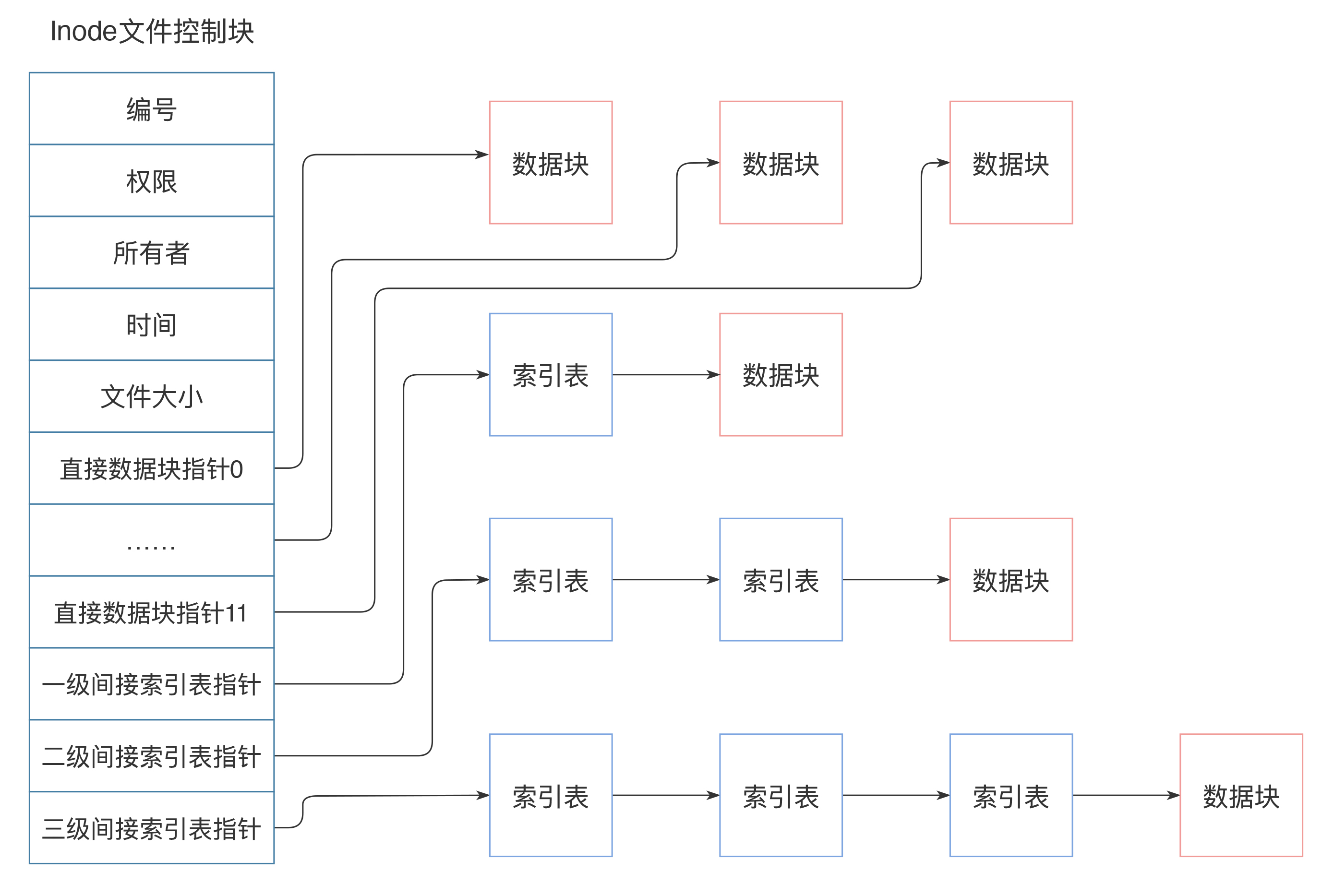
这样，每个inode最多可以存储12+256+256*256+256*256*256个数据块，如果每个数据块的大小为4k，也就是单个文件最大不超过70G，而且即使可以扩大数据块大小，文件大小也要受单个硬盘容量的限制。这样的话，对于我们开头提出的一分钟完成100T大文件的遍历，Linux文件系统是无法完成的。

那么，有没有更给力的解决方案呢？

RAID

RAID，即独立硬盘冗余阵列，将多块硬盘通过硬件RAID卡或者软件RAID的方案管理起来，使其共同对外提供服务。RAID的核心思路其实是利用文件系统将数据写入硬盘中不同数据块的特性，将多块硬盘上的空闲空间看作一个整体，进行数据写入，也就是说，一个文件的多个数据块可能写入多个硬盘。

根据硬盘组织和使用方式不同，常用RAID有五种，分别是RAID 0、RAID 1、RAID 10、RAID 5和RAID 6。we

RAID 0 将一个文件的数据分成 N 片，同时向 N 个硬盘写入，这样单个文件可以存储在 N 个硬盘上，文件容量可以扩大 N 倍，（理论上）读写速度也可以扩大 N 倍。但是使用 RAID 0 的最大问题是文件数据分散在 N 块硬盘上，任何一块硬盘损坏，就会导致数据不完整，整个文件系统全部损坏，文件的可用性极大地降低了。

RAID 1 则是利用两块硬盘进行数据备份，文件同时向两块硬盘写入，这样任何一块硬盘损坏都不会出现文件数据丢失的情况，文件的可用性得到提升。

RAID 10 结合 RAID 0 和 RAID 1，将多块硬盘进行两两分组，文件数据分成 N 片，每个分组写入一片，每个分组内的两块硬盘再进行数据备份。这样既扩大了文件的容量，又提高了文件的可用性。但是这种方式硬盘的利用率只有 50%，有一半的硬盘被用来做数据备份。

RAID 5 针对 RAID 10 硬盘浪费的情况，将数据分成 N-1 片，再利用这 N-1 片数据进行位运算，计算一片校验数据，然后将这 N 片数据写入 N 个硬盘。这样任何一块硬盘损坏，都可以利用校验片的数据和其他数据进行计算得到这片丢失的数据，而硬盘的利用率也提高到 N-1/N。

RAID 5 可以解决一块硬盘损坏后文件不可用的问题，那么如果两块文件损坏？RAID 6 的解决方案是，用两种位运算校验算法计算两片校验数据，这样两块硬盘损坏还是可以计算得到丢失的数据片。

实践中，使用最多的是 RAID 5，数据被分成 N-1 片并发写入 N-1 块硬盘，这样既可以得到较好的硬盘利用率，也能得到很好的读写速度，同时还能保证较好的数据可用性。使用 RAID 5 的文件系统比简单的文件系统文件容量和读写速度都提高了 N-1 倍，但是一台服务器上能插入的硬盘数量是有限的，通常是 8 块，也就是文件读写速度和存储容量提高了 7 倍，这远远达不到 1 分钟完成 100T 文件的遍历要求。

那么，有没有更给力的解决方案呢？

分布式文件系统

我们再回过头看下Linux的文件系统：文件的基本信息，也就是文件元信息记录在文件控制块inode中，文件的数据记录在硬盘的数据块中，inode通过索引记录数据块的地址，读写文件的时候，查询inode中的索引记录得到数据块的硬盘地址，然后访问数据。

如果将数据块的地址改成分布式服务器的地址？也就是查询得到的数据块地址不只是本机的硬盘容量，还可以是其他服务器的地址，那么文件的存储容量就将是整个分布式服务器集群的硬盘容量，这样还可以在不同的服务器上同时并行读取文件的数据块，文件访问速度也将极大的加快。

这样的文件系统就是分布式文件系统，分布式文件系统的思路其实和RAID是一脉相承的，就是将数据分成很多片，同时向N台服务器上进行数据写入。针对一片数据丢失就导致整个文件损坏的情况，分布式文件系统也是采取数据备份的方式，将多个备份数据片写入多个服务器，以保证文件的可用性。当然，也可以采用RAID 5的方式通过计算校验数据片的方式提高文件可用性。

我们以Hadoop分布式文件系统HDFS为例，看下分布式文件系统的具体架构设计。

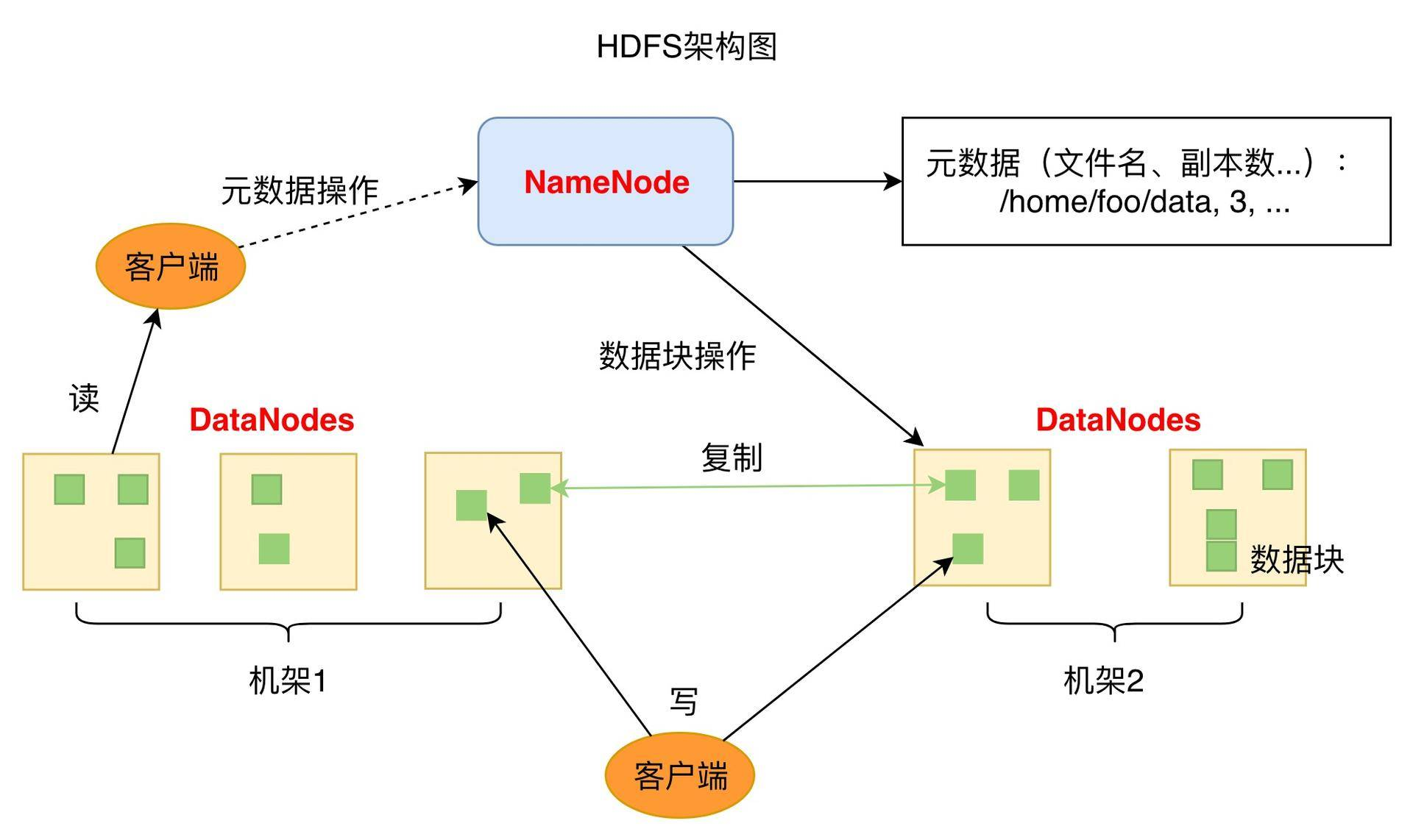
HDFS的关键组件有两个，一个是DataNode，一个是NameNode。

DataNode负责文件数据的存储和读写操作，HDFS将文件数据分隔成若干数据块（Block），每个DataNode存储一部分数据块，这样文件就分部存储在整个HDFS服务器集群中。应用程序客户端（Client）可以并行对这些数据块进行访问，从而使得HDFS可以在服务器集群规模上实现数据并行访问，极大地提高了访问速度。在实践中，HDFS集群的DataNode服务器会有很多台，一般在几百台到几千台这样的规模，每台服务器配有数块硬盘，整个集群的存储容量大概在几PB到数百PB。

NameNode负责整个分布式文件系统的元数据（MetaData）管理，也就是文件路径名、访问权限、数据块的ID以及存储位置等信息，相当于Linux系统中inode的角色。HDFS为了保证数据的高可用，会将一个数据块复制为多分（缺省情况下为3份），并将多份相同的数据块存储在不同的服务器上，甚至不同的机架上。这样当有硬盘损坏，或者某个DataNode服务器宕机，甚至某个交换机宕机，导致其存储的数据块不能访问的时候，客户端会查找其备份的数据块进行访问。

有了HDFS，可以实现单一文件存储几百T的数据，再配合大数据计算框架MapReduce或者Spark，可以对这个文件的数据块进行并发计算。也可以使用Impala这样的SQL引擎对这个文件进行结构化查询，在数千台服务器上并发遍历100T的数据，1分钟都是绰绰有余的。

小结

文件系统从简单操作系统文件，到RAID没再到分布式文件系统，其设计思路其实是具有统一性的。这种统一性方面体现在文件数据如何管理，也就是如何通过文件控制块管理文件的数据，这个文件控制块在Linux系统中就是inode，在HDFS中就是NameNode。

另一方面体现在如何利用更多的硬盘实现越来越大的文件存储需求和越来越快的读写速度需求，也就是将数据分片后同时写入多块硬盘。单服务器我们可以通过RAID来实现，多服务器则可以将这些服务器组成一个文件系统集群，共同对外提供文件服务，这时候，数千台服务器的数万块硬盘以单一存储资源的方式对文件使用提供服务，也就是一个文件可以存储数百T的数据，并在一分钟完成这样一个大文件的遍历。

思考题

在RAID 5的示意图中，P表示校验和数据，我们看到P不是单独存储在一块硬盘上，而是分散在不同的盘上，实际上，校验数据P的存储位置是螺旋式的散落在所有硬盘上的，为什么要这样设计？

1.高可用，避免检验盘损坏了所有都用不了了。 2.读取速度快，实现了检验数据的并行访问，大大加快了检验速度。

问题：

有一只青蛙，向右跳x步可以到达右边中点，向左边跳n-x步可以到达左边中点，问到达左边中点的概率。

求解方法

我们定义f(x)为到达左边中点的概率。

那么f(0) = 0，因为我们已经到达右边终点，f(n) = 1，因为我们已经到达左边终点。

我们知道，f(x) 接下来有两种走法，f(x-1)和f(x+1)，所以有

f(x) = 0.5 * f(x-1) + 0.5 * f(x+1)

我们由此可得f(x+1) - f(x) = f(x) - f(x-1)。

所以我们知道f(x)构成的序列是一个等差数列。

因为f(0) = 0, f(n) = 1，所以f(1) = 1/n，f(2) = 2/n， f(x) = x/n，f(n-1) = (n-1)/n，f(n) = n/n

所以，综上可得f(x) = x/n。

也就是说，当向右走x步到达右边终点，向左n-x步到达左边终点时，我们最后到达左边终点的概率为x/n

Splay的插入操作

正如前篇博文所讲的，Splay树是一种自平衡的数据结构，最后一个访问的键总是根。插入操作和二叉搜索树的插入类似，额外多了一些步骤来保证新插入的键称为新的根节点。

以下是插入键值k到一个Splay Tree的不同情况

1. root是空：我们简单的分配一个新的节点，并将它作为root返回
2. splay（伸展）给定的键值k。如果k已经存在，那么它称为新的根节点。如果不存在，那么最后访问的叶子节点称为新的根节点。
3. 如果新的根节点和k相同，什么都不做因为k已经存在了。
4. 否则，分配内存产生新的节点，并且将k和根的键值比较。
   1. 如果k比根的键值小，将root作为新节点的右孩子，复制root的左孩子作为新节点的左孩子，并且使root的左孩子置为NULL。
   2. 如果k比跟的键值大，将root作为新节点的左孩子，复制root的右孩子作为新节点的右孩子，并且使root的右孩子置为NULL。
5. 将新节点返回，作为整棵树的根。

感觉Splay很大程度上是可以基于AVL树进行修改的，其中左旋、右旋、左右旋、右左旋操作是相同的，只是splay有splay操作。具体实现有时间会仔细看看，在下面参考的链接中有。

参考

https://www.geeksforgeeks.org/splay-tree-set-2-insert-delete/?ref=lbp

数据结构与算法

• leetcode刷到300题啦，继续加油啊！
• 2020.08.22 第一次leetcode周赛全对，继续努力！
• 2020.08.23 leetcode周赛进了前500，继续努力！
• 2020.08.30 leetcode 204 周赛全国排名68，进入前100啦！世界排名239，进入前300啦！继续加油啊！
• 2020.09.20 leetcode 207 周赛全国排名86，继续加油啊！

生活

• 拔掉了最后两颗智齿，所有的智齿都没啦！
• 看完了《七武士》
• 读完了《被讨厌的勇气》 2020.8.26

示例解法

这道题目的dp要仔细分析。分析过程写在了注释中（个人习惯…）。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

# 我们来分析这个问题
# 我们定义f(i)为距离终点为i时所需的指令大小
# 如果i == 2 ** n - 1，指令的长度就为n
# 如果i != 2 ** n - 1，我们有两种走法
# 假设 2**(n-1) -1 < i < 2 **n - 1
# 这样n就等于i的bit_length
# 一种是走到 j = 2 ** n - 1
# 我们的指令是A^nR，指令长度为n+1，我们到终点的距离是 j-i，一定小于i
# 一种是走到 j = 2 ** (n-1) - 1, j < i
# 然后我们又往回走了 p = 2 ** k - 1, 现在我们的位置是 2 ** (n-1) - 2 ** k
# 指令长度是 A^(n-1)RA^kR n+k+1，我们现在距离终点 i - 2 **(n-1) + 2 ** k ,是小于i的
# 这样我们就得出了我们的递推公式
# f(i) = n if i == 2 ** n - 1
# f(i) = min(f(2**n -1 - i)+n+1, f(i-2**(n-1)+2**k)+n+k+1 k < n-1)
# 初始化和边界条件f(0) = 0，注意向会回走的k不会大于等于n-1，因为等于n-1时就走到0了
# 返回值f(target)
# 优化复杂度
class Solution:
    def racecar(self, target: int) -> int:
        dp = [0] + [float('inf')] * target
        for i in range(1, target + 1):
            n = i.bit_length()
            if i == (1 << n) - 1:
                dp[i] = n
            else:
                dp[i] = dp[(1 << n) - 1 - i] + n + 1
                for k in range(n - 1):
                    dp[i] = min(dp[i],
                                dp[i - (1 << (n - 1)) + (1 << k)] + n + k + 1)
        return dp[target]

合并 k 个排序链表，返回合并后的排序链表。请分析和描述算法的复杂度。

示例:

输入: [ 1->4->5, 1->3->4, 2->6] 输出: 1->1->2->3->4->4->5->6

是工业界很常见的一种操作，比如分布式系统中、数据库中，我们有多个索引是有序的，且在多个小文件中存储，我们要合并成一个新的有序链表。我们可以有哪些想法呢。

最暴力的解法是，每次遍历所有链表，找到最小的链表头，将结果链表的下一个指针指向该链表头，然后链表头指向其下一个节点。

• 时间复杂度：找最小的链表头O(k)，假设链表平均长度n，要找O(nk)次，总体是O(k^2n)的。
• 空间复杂度：O(1)，不使用额外空间

对于我来说最直接的想法是，建一个dummy哨兵链表节点，用cur指针指向dummy，同时观察所有链表的头部元素，选出最小的一个，将cur.next指向这个链表头，这个链表如果next不为Null，就加入这个链表头的集合中，否则就不加入，然后令cur=cur.next。这样加入我们共有K个链表，那么我们的集合就是K这么大，这样插入一个元素，每次删除其中最小元素都很高效的数据结构是堆。

• 总的时间复杂度就是O(k*n*logk)。因为我们一共要插入和删除K次。
• 空间复杂度：O(K)，我们要使用一个K大小的堆。

另一种想法用分治的方法进行合并。我们

• 将k个链表配对，将一对中的链表合并。
• 第一轮合并以后，k个链表被合并成了k/2个链表，平均长度为2n/k，然后是k/4个链表，k/8个链表等等。
• 重复这一过程，直到我们得到了最终的有序链表。

我们来分析一下复杂度：

• 时间复杂度：我们知道合并两个有序链表，等于两个链表长度的和，所以是O(2n)，要合并k/2个，之后合并k/4个链表，合并时间复杂度是O(4n)，所以最终的时间复杂度还是O(n k log(k)) 。
• 空间复杂度：我们归并要使用递归，递归的深度为logk，所以我们要使用O(logk)的栈空间。

示例代码

使用堆合并

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

class Solution:
    def mergeKLists(self, lists: List[ListNode]) -> ListNode:
        dummy = ListNode(0)
        cur = dummy
        # 这里的i为了排序
        heap = [(l.val, i, l) for i, l in enumerate(lists) if l]
        heapq.heapify(heap)
        while heap:
            val, ind, l = heapq.heappop(heap)
            cur.next = l
            if l.next:
                l = l.next
                heapq.heappush(heap, (l.val, ind, l))
            cur = cur.next
        return dummy.next

分支合并

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

class Solution:
    def mergeKLists(self, lists: List[ListNode]) -> ListNode:
        if not lists:
            return
        n = len(lists)
        return self.merge(lists, 0, n - 1)

    def merge(self, lists, l, r):
        if l >= r:
            return lists[l]
        mid = l + ((r - l) >> 1)
        l1 = self.merge(lists, l, mid)
        l2 = self.merge(lists, mid + 1, r)
        return self.mergeTwoLists(l1, l2)

    def mergeTwoLists(self, l1, l2):
        dummy = cur = ListNode(0)
        while l1 and l2:
            if l1.val <= l2.val:
                cur.next = l1
                l1 = l1.next
            else:
                cur.next = l2
                l2 = l2.next
            cur = cur.next
        cur.next = l1 if l1 else l2
        return dummy.next

快速排序作为一种基础的算法，广泛用于各种语言的内置排序库中，其中java使用了双基准快速排序（主要是双基准更有效的利用了计算机的缓存机制）。它是一种原地的，空间复杂度为O(1)、时间复杂度O(nlogn)、不稳定的排序算法。分为切分，和递归两个步骤。其中切分的步骤可以帮助我们以O(n)的时间复杂度找到数组中某种排名为K的元素。然而在实际实现中，快排有一些小技巧，也是我们必须要掌握的一种算法。

以下给出python版本的实现代码。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37

class Solution:
    def quickSort(self, nums: List[int]):
        return self.quickSortHelper(nums, 0, len(nums) - 1)

    def quickSortHelper(self, nums, l, r):
        if l >= r:
            return
        pivot = self.partition(nums, l, r)
        self.quickSortHelper(nums, l, pivot - 1)
        self.quickSortHelper(nums, pivot + 1, r)

    # def partition(self, nums, l, r):
    #     ran = random.randint(l, r)
    #     nums[r], nums[ran] = nums[ran], nums[r]
    #     pivot = r
    #     right = l
    #     for i in range(l, r):
    #         if nums[i] <= nums[pivot]:
    #             nums[i], nums[right] = nums[right], nums[i]
    #             right += 1
    #     nums[right], nums[pivot] = nums[pivot], nums[right]
    #     return right

    def partition(self, nums, l, r):
        ran = random.randint(l, r)
        nums[l], nums[ran] = nums[ran], nums[l]
        pivot = l
        left = r
        i = l + 1
        while i <= left:
            if nums[i] >= nums[pivot]:
                nums[i], nums[left] = nums[left], nums[i]
                left -= 1
            else:
                i += 1
        nums[left], nums[pivot] = nums[pivot], nums[left]
        return left

两个partition的效果是一样的。

注意，我们使用一种随机方法，保证了我们的快排在遇到严格递增序列或者严格递减序列的时候，期望也是O(nlogn)时间复杂度的。这是一种随机方法，还有其他随机算法的实现。这种比较简单。而这个随机的步骤，也使得我们的快排不是稳定。

题目描述

34. 在排序数组中查找元素的第一个和最后一个位置

给定一个按照升序排列的整数数组 nums，和一个目标值 target。找出给定目标值在数组中的开始位置和结束位置。

你的算法时间复杂度必须是 O(log n) 级别。

如果数组中不存在目标值，返回 [-1, -1]。

示例 1:

1
2

输入: nums = [5,7,7,8,8,10], target = 8
输出: [3,4]

示例 2:

1
2

输入: nums = [5,7,7,8,8,10], target = 6
输出: [-1,-1]

思路

这道题目当然可以给找左边界和右边界各写一个二分查找代码，因为比较简单就不写了。我们来看一下如何用一段代码找到临界索引。

我们有几个前提条件

1. 数组中可能不出现该值。
2. 数组中可能有重复元素。

我们来分析一下：

1. 对于一个元素，我们如果以插入的视角来看的话，这个元素有n+1个插入位置，对应的索引分别是0，1，2...，n。

   1. 如果我们插入的位置，左边都小于该元素，右边都大于等于该元素，那么插入位置的索引，就是第一个大于等于该元素的索引；
   2. 如果我们插入的位置，左边都小于等于该元素，右边都大于该元素，那么插入位置的索引，就是第一个大于该元素的索引，而这个索引减1，就是最后一个小于等于该元素的索引。

2. 由于数组中可能不存在该值，我们第一步求得第一个大于等于该元素的索引，

   1. 可能为n，也就是说数组中没有大于等于该值的元素
   2. 可能该索引对应的值不是等于该值，而是大于该值

   在这两种情况下，我们就不用再继续求右边的边界了。直接返回-1，-1

3. 这两种情况，仅仅是对于nums[mid] == target时，采取的策略不同，我们可以用一个参数控制不同的表现

示例代码如下：

1
2
3
4
5
6
7
8
9

def binary_search(nums, target, left):
      l, r = 0, len(nums)
       while l < r:
              mid = l + ((r - l) >> 1)
                if nums[mid] > target or (left and nums[mid] == target):
                        r = mid
               else:
                        l = mid + 1
       return l

这里返回的就是右侧集合的开始位置的下标。

示例代码

这道题的解法如下，加上了不在数组的判断

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

class Solution:
    def searchRange(self, nums: List[int], target: int) -> List[int]:
        def binary_search(nums, target, left):
            l, r = 0, len(nums)
            while l < r:
                mid = l + ((r - l) >> 1)
                if nums[mid] > target or (left and nums[mid] == target):
                    r = mid
                else:
                    l = mid + 1
            return l

        left = binary_search(nums, target, True)
        if left == len(nums) or nums[left] != target:
            return [-1, -1]
        return [left, binary_search(nums, target, False) - 1]

题目描述

给定一个非空二维矩阵 matrix 和一个整数 k，找到这个矩阵内部不大于 k 的最大矩形和。

示例:

输入: matrix = [[1,0,1],[0,-2,3]], k = 2 输出: 2 解释: 矩形区域 [[0, 1], [-2, 3]] 的数值和是 2，且 2 是不超过 k 的最大数字（k = 2）。 说明：

矩阵内的矩形区域面积必须大于 0。 如果行数远大于列数，你将如何解答呢？

思路

这道题目的思路是固定左右边界，对行进行前缀和和二分查找。

我们知道，前缀和可以让我们O(1)的时间复杂度知道任何区间和。

前缀和的典型构建方法：

1
2
3
4
5

pre = [0]
p = 0
for n in nums:
    p += n
    pre.append(p)

比如我们想知道i,j之间的区间和，包括i，j索引的话，我们的方法是pre[j+1] - pre[i]。

通过前缀和的变种，我们可以解决一些新的问题。

我们将前缀和变成hash set，就可以快速判断是否有一个区间和等于target。

我们可以插入排序的方法替换掉单纯的append，使前缀和有序，这样就可以用二分查找找到最接近某个target的区间和。

这道题目就利用了第二种想法。

我们固定左右边界，left和right，先将left到right之间的每一行的所有数值累加。这样我们就有了一列数。通过固定所有这样的left和right我们也就枚举了矩形所有的左边界和右边界。接着我们用第二种方法，边构建前缀和，编计算最接近target的矩形面积。

其大致代码如下：

1
2
3
4
5
6
7
8

pre = [0]
p = 0
for r in total:
    p += r
    loc = bisect.bisect_left(pre, p - k)
    if loc != len(pre):
        res = max(res, p - pre[loc])
    bisect.insort(pre, p)

有了这段代码，再加上我们固定左右边界的代码，我们就可以解决这个问题。计算一下复杂度。

固定左右边界需要O(n^2)的时间复杂度，n为矩形的列数。生成前缀和遍历需要O(m)，m为矩阵的行数，搜索是O(logm)的，但是插入是O(m)的。所以总体上还是O(n^2m^2)的。但是常数项比较低。

总体代码如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

class Solution:
    def maxSumSubmatrix(self, matrix: List[List[int]], k: int) -> int:
        m, n = len(matrix), len(matrix[0])
        total = [0] * m
        res = float('-inf')
        for left in range(n):
            total[:] = [0] * m
            for right in range(left, n):
                for i in range(m):
                    total[i] += matrix[i][right]
                pre = [0]
                p = 0
                for r in total:
                    p += r
                    loc = bisect.bisect_left(pre, p - k)
                    if loc != len(pre):
                        res = max(res, p - pre[loc])
                    bisect.insort(pre, p)
        return res

另一道相似题目

1546. 和为目标值的最大数目不重叠非空子数组数目

给你一个数组 nums 和一个整数 target 。

请你返回 非空不重叠 子数组的最大数目，且每个子数组中数字和都为 target 。

示例 1：

输入：nums = [1,1,1,1,1], target = 2 输出：2 解释：总共有 2 个不重叠子数组（加粗数字表示） [1,1,1,1,1] ，它们的和为目标值 2 。 示例 2：

输入：nums = [-1,3,5,1,4,2,-9], target = 6 输出：2 解释：总共有 3 个子数组和为 6 。 ([5,1], [4,2], [3,5,1,4,2,-9]) 但只有前 2 个是不重叠的。 示例 3：

输入：nums = [-2,6,6,3,5,4,1,2,8], target = 10 输出：3 示例 4：

输入：nums = [0,0,0], target = 0 输出：3

提示：

1 <= nums.length <= 10^5 -10^4 <= nums[i] <= 10^4 0 <= target <= 10^6

这道题目就是使用了第一种前缀和的变化，并应用了贪心的思想。

一旦发现target在区间和中，我们就重新统计前缀和。示例代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14

class Solution:
    def maxNonOverlapping(self, nums: List[int], target: int) -> int:
        pre = {0}
        p = 0
        res = 0
        for n in nums:
            p += n
            if p - target in pre:
                res += 1
                pre = {0}
                p = 0
            else:
                pre.add(p)
        return res

二叉搜索树最坏的时间复杂度比如查找、删除、插入是O(n)的。最坏的情况发生在这棵树已经倾斜了。我们可以使最坏情况的时间复杂度也为O(logn)使用AVL和红黑树。

我们可以比AVL和红黑树在实践中做得更好吗？

像AVL和红黑树一样，splay tree也是自平衡二叉搜索树。splay tree的主要思想是将最近访问的项目放到树的根节点，这使得最近搜索过的项目可以在O(1)的时间复杂度内被搜索到，如果它再次被搜索。思想是使用访问的局部性（在一个典型的应用中，80%的访问是访问其中20%的项目）。想象一个场景，我们有数百万或数十亿的键但是只有它们中很少一部分会被经常访问，这在实际应用中非常有可能发生。

所有的splay tree操作都平均是O(logn)时间复杂度的，n是树中节点的数量。任何一个操作在最坏的情况下可能使用Theta(n)的时间。

查找操作

splay tree的查找操作使用标准的BST查找，在查找同时，它同时还伸展（splay）（将一个节点移到根）。如果查找是成功的，那么找到的那个节点就被伸展并成为新根节点。否则，在到达NULL之前最后被访问的节点被伸展并成为新的根节点。

被访问的节点有以下几种情况。

1. 节点是根节点。我们简单地返回根节点，不会做任何事，因为访问的节点已经是根节点。

2. Zig：节点是root的子节点（该节点没有祖父母）。节点要么是根的左子节点（我们做右旋），要么是根的右子节点（我们做左旋）。

   T1，T2和T3是树的子树，其根为y（在左侧）或x（在右侧）。

1
2
3
4
5

    y                                     x
   / \     Zig (Right Rotation)          /  \
  x   T3   – - – - – - – - - ->         T1   y 
 / \       < - - - - - - - - -              / \
T1  T2     Zag (Left Rotation)            T2   T3

3. 节点既有父节点，也有祖父节点。可以有以下几种情况。

   3.a. Zig-Zig和Zag-Zag 节点是父节点的左儿子而且父节点同样也是祖父节点的左儿子（两次右旋），或者，节点是父节点的右儿子而且父节点也是祖父节点的右儿子（两次左旋）。

   1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17

   Zig-Zig (Left Left Case): G P X / \ / \ / \ P T4 rightRotate(G) X G rightRotate(P) T1 P / \ ============> / \ / \ ============> / \ X T3 T1 T2 T3 T4 T2 G / \ / \ T1 T2 T3 T4 Zag-Zag (Right Right Case): G P X / \ / \ / \ T1 P leftRotate(G) G X leftRotate(P) P T4 / \ ============> / \ / \ ============> / \ T2 X T1 T2 T3 T4 G T3 / \ / \ T3 T4 T1 T2

   3.b. Zig-Zag and Zag-Zig 节点是父节点的左儿子，父节点是祖父节点的右儿子（左旋，接着右旋），或者，节点父节点的右儿子，父节点是祖父节点的左儿子（右旋，接着左旋）。

   1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17

   Zag-Zig (Left Right Case): G G X / \ / \ / \ P T4 leftRotate(P) X T4 rightRotate(G) P G / \ ============> / \ ============> / \ / \ T1 X P T3 T1 T2 T3 T4 / \ / \ T2 T3 T1 T2 Zig-Zag (Right Left Case): G G X / \ / \ / \ T1 P rightRotate(P) T1 X leftRotate(P) G P / \ =============> / \ ============> / \ / \ X T4 T2 P T1 T2 T3 T4 / \ / \ T2 T3 T3 T4

例子

1
2
3
4
5
6
7
8
9

         100                      100                       [20]
         /  \                    /   \                        \ 
       50   200                50    200                      50
      /          search(20)    /          search(20)         /  \  
     40          ======>     [20]         ========>         30   100
    /            1. Zig-Zig    \          2. Zig-Zig         \     \
   30               at 40       30            at 100         40    200  
  /                               \     
[20]                              40

需要注意的是，搜索或splay操作不仅将被搜索的键带到了根节点，还平衡了BST。例如在上面的案例中，BST的高度减少了1。

实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156

#include <bits/stdc++.h> 
using namespace std; 

// An AVL tree node 
class node 
{ 
    public: 
 int key; 
    node *left, *right; 
}; 

/* Helper function that allocates 
a new node with the given key and 
  NULL left and right pointers. */
node* newNode(int key) 
{ 
 node* Node = new node(); 
    Node->key = key; 
  Node->left = Node->right = NULL; 
  return (Node); 
} 

// A utility function to right 
// rotate subtree rooted with y 
// See the diagram given above. 
node *rightRotate(node *x) 
{ 
  node *y = x->left; 
    x->left = y->right; 
    y->right = x; 
 return y; 
} 

// A utility function to left 
// rotate subtree rooted with x 
// See the diagram given above. 
node *leftRotate(node *x) 
{ 
 node *y = x->right; 
   x->right = y->left; 
    y->left = x; 
  return y; 
} 

// This function brings the key at 
// root if key is present in tree. 
// If key is not present, then it 
// brings the last accessed item at 
// root. This function modifies the 
// tree and returns the new root 
node *splay(node *root, int key) 
{ 
 // Base cases: root is NULL or 
  // key is present at root 
   if (root == NULL || root->key == key) 
       return root; 

  // Key lies in left subtree 
 if (root->key > key) 
  { 
       // Key is not in tree, we are done 
      if (root->left == NULL) return root; 

     // Zig-Zig (Left Left) 
      if (root->left->key > key) 
     { 
           // First recursively bring the 
          // key as root of left-left 
         root->left->left = splay(root->left->left, key); 

           // Do first rotation for root, 
          // second rotation is done after else 
           root = rightRotate(root); 
        } 
       else if (root->left->key < key) // Zig-Zag (Left Right) 
      { 
           // First recursively bring 
          // the key as root of left-right 
            root->left->right = splay(root->left->right, key); 

         // Do first rotation for root->left 
          if (root->left->right != NULL) 
               root->left = leftRotate(root->left); 
       } 

     // Do second rotation for root 
      return (root->left == NULL)? root: rightRotate(root); 
   } 
   else // Key lies in right subtree 
  { 
       // Key is not in tree, we are done 
      if (root->right == NULL) return root; 

        // Zag-Zig (Right Left) 
     if (root->right->key > key) 
        { 
           // Bring the key as root of right-left 
          root->right->left = splay(root->right->left, key); 

         // Do first rotation for root->right 
         if (root->right->left != NULL) 
               root->right = rightRotate(root->right); 
        } 
       else if (root->right->key < key)// Zag-Zag (Right Right) 
     { 
           // Bring the key as root of 
         // right-right and do first rotation 
            root->right->right = splay(root->right->right, key); 
         root = leftRotate(root); 
     } 

     // Do second rotation for root 
      return (root->right == NULL)? root: leftRotate(root); 
   } 
} 

// The search function for Splay tree. 
// Note that this function returns the 
// new root of Splay Tree. If key is 
// present in tree then, it is moved to root. 
node *search(node *root, int key) 
{ 
  return splay(root, key); 
} 

// A utility function to print 
// preorder traversal of the tree. 
// The function also prints height of every node 
void preOrder(node *root) 
{ 
    if (root != NULL) 
  { 
       cout<<root->key<<" "; 
     preOrder(root->left); 
     preOrder(root->right); 
    } 
} 

/* Driver code*/
int main() 
{ 
   node *root = newNode(100); 
   root->left = newNode(50); 
 root->right = newNode(200); 
   root->left->left = newNode(40); 
    root->left->left->left = newNode(30); 
   root->left->left->left->left = newNode(20); 

    root = search(root, 20); 
 cout << "Preorder traversal of the modified Splay tree is \n"; 
 preOrder(root); 
  return 0; 
} 

// This code is contributed by rathbhupendra 

输出

1
2

Preorder traversal of the modified Splay tree is
20 50 30 40 100 200

总结

1. splay tree有优异的局部性特质。经常访问的元素很容易被找到。不长访问的元素都不在查找的路上。
2. 所有的splay操作都平均使用O(logn)的时间复杂度。splay tree可以严格的证明，在任何操作的序列上，每次操作的平均时间为O(logn)（假设我们从一颗空树开始）。
3. splay tree与AVL树和红黑树相比更简单，因为每个树节点都不需要额外的空间。
4. 与AVL树不同，splay树即使进行搜索操作等只读操作也可能改变。

splay tree 的应用场景

splay tree已经成为了过去30年中发明的应用最广泛的基本数据结构，因为它是许多应用中最快的平衡搜索树类型。splay tree被用于Windows NT（在虚拟内存、网络和文件系统代码中）、gcc编译器和GNU C++库、sed字符串编辑器、Fore Systems网络路由器、Unix malloc最流行的实现、Linux可加载的内核模块和许多其他软件中（来源：http://www.cs.berkeley.edu/~jrs/61b/lec/36）。

参考

https://www.geeksforgeeks.org/splay-tree-set-1-insert/?ref=lbp

下一节我们讲splay的插入操作