侯瑞哲的博客

Ruizhe's Blog

0%

Tarjan寻找图的强连通分量算法

发表于 更新于 Valine：

参考

  • GeeksforGeeks

如果所有的顶点对之间都有一条路径，那么一个有向图就是强连通的。有向图的强连通分量（strongly connected component，SCC）是一个最大强连通子图。例如，下面的图中有3个SCC。

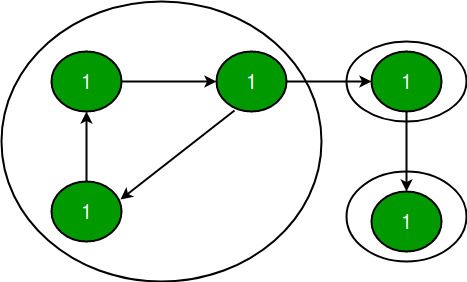
我们已经讨论过Kosaraju的强连通分量的算法。前面讨论的算法需要对一个Graph进行两次DFS遍历。在这篇文章中，我们将讨论Tarjan算法，它只需要一次DFS遍历。

Tarjan算法基于以下事实：

  1. DFS搜索会产生一个DFS树/森林；
  2. 强连通分量构成DFS树的子树；
  3. 如果我们能找到这种子树的头，就可以打印/存储该子树的所有结点（包括头），这将是一个SCC；
  4. 从一个SCC到另一个SCC没有回溯边（back edge）（可以有交叉边，但在处理图的时候不会用到交叉边）。

为了找到一个SCC的头部，我们要计算disc和low数组（就像处理衔接点、桥、双连接组件一样）。如前几篇文章所讨论的，low[u]表示从以u为根的子树中可以到达的最早被访问的顶点（发现时间最短的顶点），如果disc[u]=low[u]，则节点u为头部。

下图是该方法的说明：

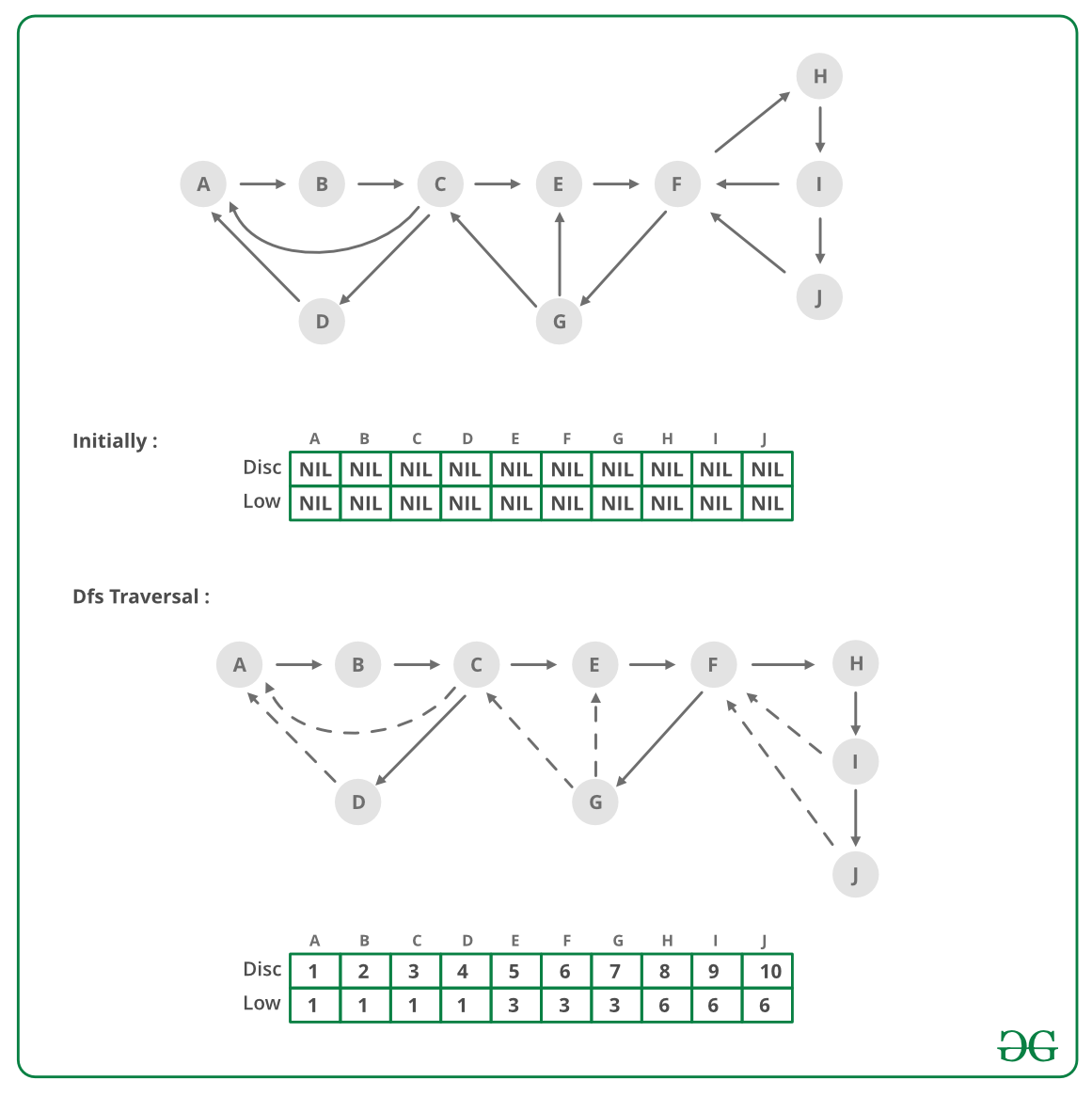
强连通分量只与有向图有关，但Disc和Low值与有向图和无向图都有关。

在上图中，我们展示了一个图形和它的一颗DFS树（在同一个图形上可以有不同的DFS树，取决于边被遍历的顺序）。在DFS树中，连续的箭头是树的边，虚线的箭头是back edge

图中每个节点的disc和low的值显示为disc/low

Disc: 是指在DFS遍历时，节点第1次被访问的时间。这是在DFS遍历时，一个节点第一次被访问的时间。对于DFS树中的节点A，B，C，...，J，Disc值为1，2，3，…，10。

Low: 在DFS树中，树边带我们向前走，从祖先节点到它的一个子孙节点。例如，从节点C开始，树边可以带我们到节点G、节点I等。回溯边（back edge）带我们往后走，从一个子孙节点到它的一个祖先节点，例如，从节点G出发，back edge带我们到E或C。如果我们把树边和回溯边（back edge）一起看，那么我们可以看到，如果我们从一个节点开始遍历，我们可能会通过树边向下走，然后通过回溯边向上走。例如，从节点E开始，我们可以向下走到I或J，然后向上走到F。一个节点的Low值告诉了我们通过该节点的子树所能到达的最顶层祖先（最小可能的disc值）。所以对于任何一个节点，无论如何Low值都等于它的Disc值（一个节点是它自己的祖先）。然后我们查看它的子树，看看是否有任何节点可以带我们找到它的任何一个祖先。如果在子树中有多条回溯边可以带我们到不同的祖先，那么我们就选取Disc值最小的那条（即最上面的那条）。如果我们看一下节点F，它有两个子树。有节点G的子树，把我们带到E和C，另一个子树只把我们带回F。这里最顶层的祖先是F可以到达的C，所以F的Low值是3（C的Disc值）。

根据上面的讨论，应该很清楚，B、C、D的Low值是1（因为A是B、C、D可以到达的最上面的节点）。同理，E、F、G的Low值为3，H、I、J的Low值为6。

对于任何节点u，当DFS开始时，Low将会被设置为其Disc 1st。

然后对它的每一个子节点v依次进行DFS，u的Low值可以在两种情况下改变：

  • Case1（Tree Edge）：如果节点v还没有被访问，那么在v的DFS完成后，low[u] = min(low[u], low[v])
  • Case2（Back Edge）：当后代v已经被访问，那么low[u] = min(low[u], disc[v]);

在第二种情况下，我们是否可以用low[v]代替DIsc[v]？答案是NO。如果你能想到为什么答案是NO，那么你大概明白Low和Disc的概念。（因为是有向图，low[v]是v能访问到的最小节点，u不一定能访问到，u能访问到v，说明disc[v]一定是可以取到的）

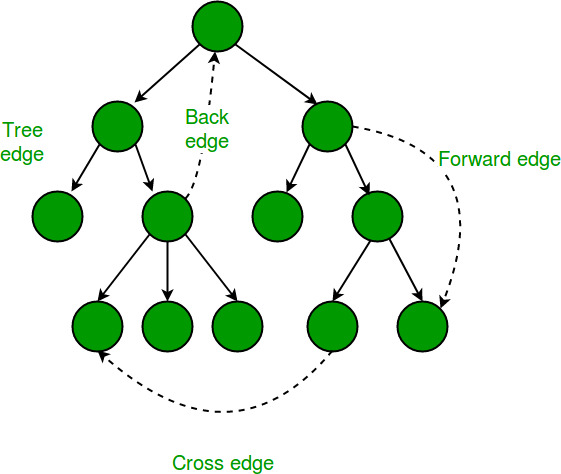
相同的Low和Disc值有助于解决其他图的问题，如衔接点、桥和双连接分量。

为了跟踪以头部为根的子树，我们可以使用栈（在访问时不断推送节点）。当发现一个头部节点时，从堆栈中弹出所有节点，直到从栈中得到头部。

为了确保不考虑交叉边，当我们到达一个已经被访问过的节点时，只有当栈中存在被访问过的节点时，我们才应该对该节点进行处理，否则忽略该节点。

实现：写一个Tarjan算法找到有向图的所有连通分量并打印出来

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
class Graph:
    def __init__(self, vertices):
        self.V = vertices
        self.neigh = defaultdict(list)
        self.Time = 0

    def addEdge(self, x, y):
        self.neigh[x].append(y)

    def scc(self):
        disc = [-1] * self.V
        low = [-1] * self.V
        visited = [False] * self.V
        stack = []
        for i in range(self.V):
            if disc[i] == -1:
                self.scc_util(i, low, disc, visited, stack)

    def scc_util(self, u, low, disc, visited, stack):
        disc[u] = self.Time
        low[u] = self.Time
        self.Time += 1
        visited[u] = True
        stack.append(u)
        for v in self.neigh[u]:
            if disc[v] == -1:
                self.scc_util(v, low, disc, visited, stack)
                low[u] = min(low[u], low[v])
            elif visited[v]:
                low[u] = min(low[u], disc[v])
        w = -1
        if disc[u] == low[u]:
            while w != u:
                w = stack.pop()
                print(w, end=' ')
                visited[w] = False
            print()


def main():
    g1 = Graph(5)
    g1.addEdge(1, 0)
    g1.addEdge(0, 2)
    g1.addEdge(2, 1)
    g1.addEdge(0, 3)
    g1.addEdge(3, 4)
    print("SCC in first graph")
    g1.scc()

    g2 = Graph(4)
    g2.addEdge(0, 1)
    g2.addEdge(1, 2)
    g2.addEdge(2, 3)
    print("SCC in second graph")
    g2.scc()

    g3 = Graph(7)
    g3.addEdge(0, 1)
    g3.addEdge(1, 2)
    g3.addEdge(2, 0)
    g3.addEdge(1, 3)
    g3.addEdge(1, 4)
    g3.addEdge(1, 6)
    g3.addEdge(3, 5)
    g3.addEdge(4, 5)
    print("SCC in third graph")
    g3.scc()

    g4 = Graph(11)
    g4.addEdge(0, 1)
    g4.addEdge(0, 3)
    g4.addEdge(1, 2)
    g4.addEdge(1, 4)
    g4.addEdge(2, 0)
    g4.addEdge(2, 6)
    g4.addEdge(3, 2)
    g4.addEdge(4, 5)
    g4.addEdge(4, 6)
    g4.addEdge(5, 6)
    g4.addEdge(5, 7)
    g4.addEdge(5, 7)
    g4.addEdge(5, 8)
    g4.addEdge(5, 9)
    g4.addEdge(6, 4)
    g4.addEdge(7, 9)
    g4.addEdge(8, 9)
    g4.addEdge(9, 8)
    print("SCC in forth graph")
    g4.scc()

    g5 = Graph(5)
    g5.addEdge(0, 1)
    g5.addEdge(1, 2)
    g5.addEdge(2, 3)
    g5.addEdge(2, 4)
    g5.addEdge(3, 0)
    g5.addEdge(4, 2)
    print("SCC in fifth graph")
    g5.scc()


if __name__ == '__main__':
    main()

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
# Output
SCC in first graph
4 
3 
1 2 0 
SCC in second graph
3 
2 
1 
0 
SCC in third graph
5 
3 
4 
6 
2 1 0 
SCC in forth graph
8 9 
7 
5 4 6 
3 2 1 0 
10 
SCC in fifth graph
4 3 2 1 0

时间复杂度：算法主要使用DFS，邻接表表示的图的DFS算法是O(V+E)复杂度的。