Prim算法是一种Greedy算法。它从一个空的生成树开始。其想法是维护两组顶点。第一组包含已经在MST中的顶点,另一组包含尚未在的顶点。在每一步,它都会考虑连接两组的所有边,并从这些边中挑选出最小权重的边。选取边后,它将边的另一个顶点移动到包含MST的集合中。
在图论中,连接两组顶点的一组边被称为切边(cut)。所有,在Prim算法的每一步,我们都要要找到一个cut(关于这两个集合的,一个包含已经在MST中的顶点,另一个包含其余的顶点),从cut中挑选出最小权重的边,并将这个顶点包含到MST集合(包含已经在MST中的顶点)中。
Prim's Algorithm是如何工作的?Prim算法背后的思想很简单,一颗生成树意味着所有顶点必须是连接的。所以,两个不相干的顶点子集(上面讨论的)必须连接起来,才能组成一个生成树。而且它们必须用最小的权重边连接起来,才能使之成为一颗最小生成树。
算法:
- 创建一个集合mstSet,用来跟踪已经包含在MST中的顶点。
- 给输入图中的所有顶点分配一个键值。初始化所有的键值为infinity。为第一个顶点分配键值为0,这样它就会被首先选中。
- while mstSet不包含所有的顶点
- 选取一个在mstSet中没有的顶点u,并且其键值最小。
- 将u加入到mstSet中。
- 更新u的所有相邻顶点的键值,更新键值时,要遍历所有相邻顶点。对于每一个相邻顶点v,如果边u-v的权重小于v的前一个键值,则更新键值为u-v的权重。
使用键值的想法是为了从cut中挑选出最小权重的边。键值只用于尚未包含在MST中的顶点,这些顶点的键值表示连接它们与MST中包含的顶点集的最小权重边的权重。
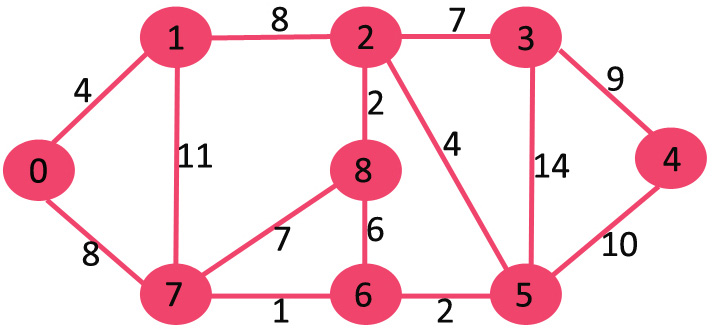
集合mstSet开始的时候是空的,并且每个顶点键值时{0, INF, INF, INF, INF, INF, INF, INF},INF表示无穷大。现在,选出一个拥有最小键值的顶点。顶点0被选出,将其放入mstSet。所以mstSet成为了{0}。在包括进mstSet之后,更新相邻顶点的键值。0的相邻顶点是1和7。1和7的键值被更新为4和8。下面的子图显示了顶点和它们的键值,只有有有限键值的顶点展示了出来。在MST中的顶点用绿颜色表示了出来。
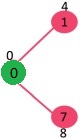
选出有最小键值的顶点并且还没有被包括进MST(还不在mstSet)。顶点1被选出来,并且被加入mstSet。所以mstSet成为了{0, 1}。更新1的相邻顶点的键值。顶点2的键值变成了8。
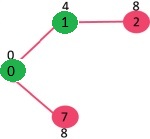
选出具有最小键值的顶点,并且还没有包含在MST中(不在mstSet中)。我们可以选择顶点7或者2,我们让7被选中。所以mstSet现在变成了{0, 1, 7}。更新7的相邻顶点的键值,顶点6和8的键值变成了有限的(分别为1和7)。
选出具有最小键值的顶点,并且还没有包含在MST中(不在mstSet中)。顶点6被选中。所以mstSet现在为{0, 1, 7, 6}。更新6的相邻顶点的键值。5和8的键值被更新。
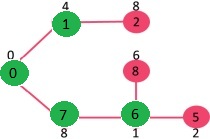
我们重复上面的步骤直到mstSet包含了给定图中所有的顶点。最终,我们得到了如下的图。
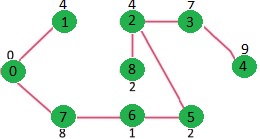
如何实现上面的算法?
我们用一个布尔数组mstSet[]表示MST中包含的顶点集合。如果一个值mstSet[v]为true,那么顶点v就在MST中,否则就不是。数组key[]用来存储所有顶点的键值。另一个数组parent[]用来存储MST中父节点的索引。parent数组是输出数组,用来显示构建的MST。
上面算法的时间复杂度为O(V^2)。如果使用邻接表表示输入图,那么在二叉堆的帮助下,Prim算法的时间复杂度可以降低到O(ElogV)。