上一篇中介绍了旅行商问题,并讨论了该问题的朴素和DP解决方案。这两种解决方案都是不可行的。事实上,这个问题没有多项式时间的解决方案,因为这个问题是一个已知的NP-Hard问题。不过有近似算法可以解决这个问题。近似算法只有在问题满足三角形不等式的情况下才有效。
三角形不等式:从顶点i到顶点j的最短路径总是直接从i到达j,而不是通过其他顶点k,即dist(i, j)总是小于等于dist(i, k) + dist(k, j)。三角形不等式在很多情况下都是成立的。当成本函数满足三角形不等式时,我们可以为TSP设计一个近似算法,该算法返回的旅游成本永远不会超过最优旅游成本的两倍。其思想是使用最小生成树(Minimum Spanning Tree, MST)。以下是基于MST的算法。
算法
- 让1成为销售员的起点和终点。
- 用Prim's Algorithm以1为根构建MST。
- 列出构造的MST的前序遍历中所访问的顶点,并在最后添加1.
让我们考虑下面的例子。第一张图是给定的图,第二张图是以1为根构建的MST。MST的前序遍历是1-2-4-3。在末尾加1,得到1-2-4-3-1,这就是这个算法的输出。
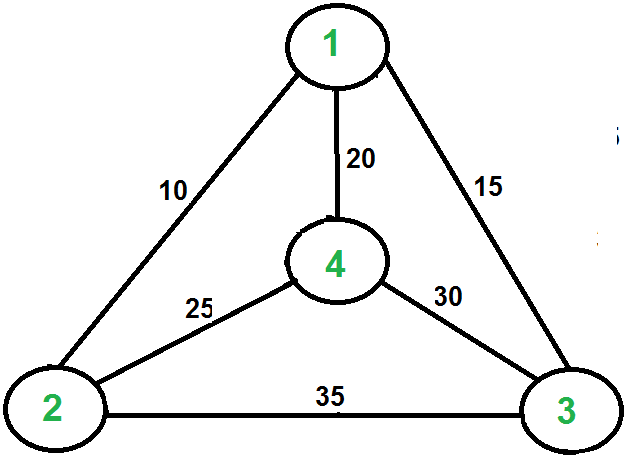
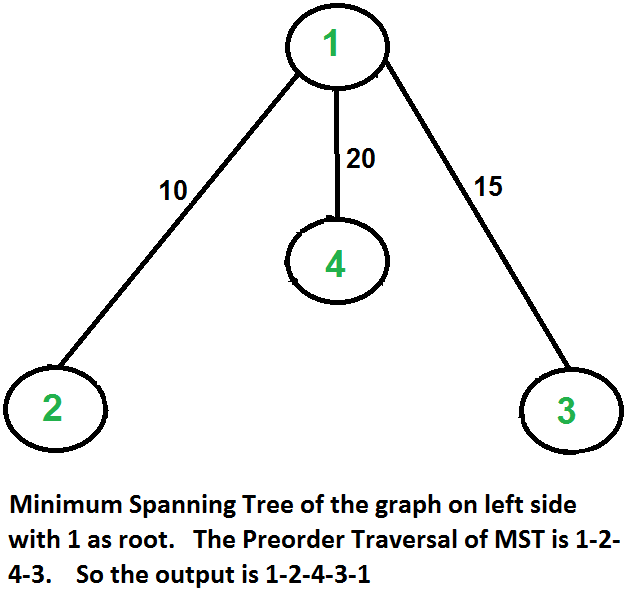
这种情况下,近似算法会产生最优线路,但未必在所有情况下都能产生最优路径。
这个算法是如何2倍近似的?上述算法产生的输出成本永远不会超过最佳可能输出成本的两倍。我们来看看上述算法是如何保证这一点的。
让我们定义一个术语"full walk"来理解这个问题。一个full walk是当一个顶点被前序遍历访问访问时列出它们,并且当某个顶点的子树被返回时也列出这些顶点。上面树的full walk将是1-2-1-4-1-3-1。下面是证明2-近似性的一些重要事实。
- 最好的旅行商路线的成本绝不小于MST的成本。(MST的定义说,它是连接所有顶点的最小成本树。)
- full walk的总成本最多是MST成本的两倍(MST的每条边最多被访问两次)。
- 上述算法的输出小于full walk的成本。在上面的算法中,我们打印出preorder walk作为输出。在前序遍历中,full walk的两条或多条边被一条边所取代。例如,2-1和1-4被一条边2-4所取代。所以,如果图形遵循三角形不等式,那么这条结论总是对的。
从以上三句陈述中,我们可以得出结论,近似算法产生的输出成本永远不会超过最佳可能解成本的两倍。
我们讨论了一个非常简单的旅行商问题的2-近似算法。对于这个问题还有其他更好的近似算法。例如Christofides算法是1.5近似算法。我们将很快把这些算法作为单独的文章来讨论。
参考
https://www.geeksforgeeks.org/travelling-salesman-problem-set-2-approximate-using-mst/?ref=lbp