旅行商问题（朴素和dp方法）

Travelling Salesman Problem(TSP)旅行商问题：给定一个集合的城市和每一对城市之间的距离，问题是找到最短可能的路径，访问每个城市恰好一次，并且返回出发的城市。

注意汉密尔顿循环问题和TSP问题的区别。汉密尔顿循环问题是要找到是否存在一条完全访问每个城市一次的旅游路线。这里我们知道汉密尔顿循环路线存在（因为图是完整的），事实上很多这样的环存在，问题是找到一个最小权重的汉密尔顿循环。

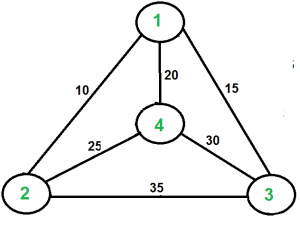
比如，考虑右图所示的图形。图中一个TSP循环是1-2-4-3-1。旅行的费用是10+25+30+15即80。

这个问题是一个著名的NP问题。这个问题没有多项式时间的已知解。

以下是旅行商问题的不同解法。

朴素的解法：

将城市1作为起点和终点
生成所有（n-1）！城市的排列组合
计算每个排列组合的成本，并跟踪成本最小的排列组合
返回成本最小的排列组合

时间复杂度：O(n!)

DP 动态递推

让给定的顶点集为{1, 2, 3, 4, ..., n}。让我们把1作为输出的起点和终点。对于每一个其他的顶点i（1除外），我们找到以1为起点，i为终点，且所有顶点只出现一次的最小成本路径。让这条路径的成本为cost(i)。对应CUcle的成本将是cost(i) + dist(i, 1)，其中dist(i, 1)是i到1的距离。最后我们返回所有[cost(i) + dist(i, 1)]值的最小值。到目前为止，这看起来很简单。现在的问题是如何得到cost(i)？

为了使用DP计算cost(i)，我们需要在子问题方面有一些地推关系。让我们定义一个术语C(S, i)为从1开始，到i结束，精确访问集S中每个顶点一次的最小成本路径的成本。我们从大小为2的所有子集开始，计算S为子集的所有子集的C(S, i)，然后我们计算大小为3的所有子集S的C(S, i)，以此类推。注意，每个子集中必须有1.

If size of S is 2, then S must be {1, i},
 C(S, i) = dist(1, i) 
Else if size of S is greater than 2.
 C(S, i) = min { C(S-{i}, j) + dist(j, i)} where j belongs to S, j != i and j != 1.

对于一个大小为n的集合，我们考虑每个大小为n-1的n-2个子集，使所有子集中没有t（代表集合的排序）。

利用上述递归关系，我们可以写出基于DP的解决方案。最多有O(n*2^n)个子问题，每个子问题的求解都需要线性时间。因此，总的运行时间是O(n^2*2^n)。时间复杂度远小于O(n!)，但仍是指数级的。所需空间也是指数级的。所以这种方法即使对于稍高的顶点数量也是不可行的。

我们很快就会讨论旅行推销员问题的近似算法。

参考：

https://www.geeksforgeeks.org/travelling-salesman-problem-set-1/