线段树 | 侯瑞哲的博客

参考：

https://zh.wikipedia.org/wiki/%E7%B7%9A%E6%AE%B5%E6%A8%B9

https://www.geeksforgeeks.org/segment-tree-set-1-sum-of-given-range/

原文我觉得挺不错的，暂时觉得先不翻译。

链接

实际问题（简单记，想快速知道数组的某一区间和，同时数组的修改频繁，使得这两种操作都变成O(logn)，用线段树，可利用思想解决最大子段和问题）

Let us consider the following problem to understand Segment Trees.

We have an array arr[0 . . . n-1]. We should be able to 1 Find the sum of elements from index l to r where 0 <= l <= r <= n-1

2 Change value of a specified element of the array to a new value x. We need to do arr[i] = x where 0 <= i <= n-1.

A simple solution is to run a loop from l to r and calculate the sum of elements in the given range. To update a value, simply do arr[i] = x. The first operation takes O(n) time and the second operation takes O(1) time.

Another solution is to create another array and store sum from start to i at the ith index in this array. The sum of a given range can now be calculated in O(1) time, but update operation takes O(n) time now. This works well if the number of query operations is large and very few updates.

给定一个数组，我们既想快速的知道任意一段区间的总和是多少，也想经常改变其中任何一个元素的值。

第一种解决办法就是，对每一个l和r，我们计算l和r之间的和，O(n)的复杂度，改变其中任何一个值，O(1)的时间复杂度。

第二种解决办法就是，我们创建好另一个数组，存储从开始到这个索引的元素和是多少，（前缀和，通常前缀和在数组的前面加上一个0，这样所有lr之间的和等于这个_sum数组的 _sum[r] - _sum[l-1]）。这样求l到r之间的和就变成O(1)的时间复杂度了，但是每改变一个值就变成O(n)的了。

What if the number of query and updates are equal? Can we perform both the operations in O(log n) time once given the array? We can use a Segment Tree to do both operations in O(Logn) time.

Representation of Segment trees 1. Leaf Nodes are the elements of the input array. 2. Each internal node represents some merging of the leaf nodes. The merging may be different for different problems. For this problem, merging is sum of leaves under a node.

An array representation of tree is used to represent Segment Trees. For each node at index i, the left child is at index 2i+1, right child at 2i+2 and the parent is at .

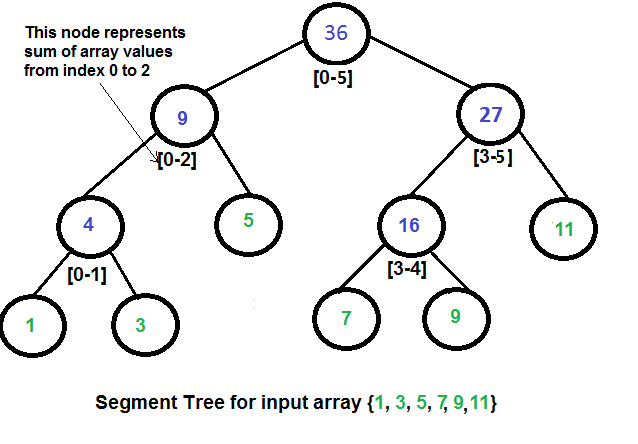
How does above segment tree look in memory? Like Heap, the segment tree is also represented as an array. The difference here is, it is not a complete binary tree. It is rather a full binary tree (every node has 0 or 2 children) and all levels are filled except possibly the last level. Unlike Heap, the last level may have gaps between nodes. Below are the values in the segment tree array for the above diagram.

Below is memory representation of segment tree for input array {1, 3, 5, 7, 9, 11} st[] = {36, 9, 27, 4, 5, 16, 11, 1, 3, DUMMY, DUMMY, 7, 9, DUMMY, DUMMY}

The dummy values are never accessed and have no use. This is some wastage of space due to simple array representation. We may optimize this wastage using some clever implementations, but code for sum and update becomes more complex.

Construction of Segment Tree from given array We start with a segment arr[0 . . . n-1]. and every time we divide the current segment into two halves(if it has not yet become a segment of length 1), and then call the same procedure on both halves, and for each such segment, we store the sum in the corresponding node. All levels of the constructed segment tree will be completely filled except the last level. Also, the tree will be a Full Binary Tree because we always divide segments in two halves at every level. Since the constructed tree is always a full binary tree with n leaves, there will be n-1 internal nodes. So the total number of nodes will be 2*n – 1. Note that this does not include dummy nodes.

What is the total size of the array representing segment tree? If n is a power of 2, then there are no dummy nodes. So the size of the segment tree is 2n-1 (n leaf nodes and n-1) internal nodes. If n is not a power of 2, then the size of the tree will be 2*x – 1 where x is the smallest power of 2 greater than n. For example, when n = 10, then size of array representing segment tree is 2*16-1 = 31. An alternate explanation for size is based on heignt. Height of the segment tree will be . Since the tree is represented using array and relation between parent and child indexes must be maintained, size of memory allocated for segment tree will be .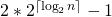

Query for Sum of given range Once the tree is constructed, how to get the sum using the constructed segment tree. The following is the algorithm to get the sum of elements.

int getSum(node, l, r) 
{
   if the range of the node is within l and r
        return value in the node
   else if the range of the node is completely outside l and r
        return 0
   else
    return getSum(node's left child, l, r) + 
           getSum(node's right child, l, r)
}

Update a value Like tree construction and query operations, the update can also be done recursively. We are given an index which needs to be updated. Let diff be the value to be added. We start from the root of the segment tree and add diff to all nodes which have given index in their range. If a node doesn’t have a given index in its range, we don’t make any changes to that node.

Implementation: Following is the implementation of segment tree. The program implements construction of segment tree for any given array. It also implements query and update operations.

# Python3 program to show segment tree operations like 
# construction, query and update 
from math import ceil, log2; 

# A utility function to get the 
# middle index from corner indexes. 
def getMid(s, e) : 
   return s + (e -s) // 2; 

""" A recursive function to get the sum of values 
   in the given range of the array. The following 
   are parameters for this function. 

  st --> Pointer to segment tree 
    si --> Index of current node in the segment tree. 
     Initially 0 is passed as root is always at index 0 
   ss & se --> Starting and ending indexes of the segment 
                represented by current node, i.e., st[si] 
    qs & qe --> Starting and ending indexes of query range """
def getSumUtil(st, ss, se, qs, qe, si) : 

    # If segment of this node is a part of given range, 
 # then return the sum of the segment 
    if (qs <= ss and qe >= se) : 
     return st[si]; 

    # If segment of this node is 
    # outside the given range 
   if (se < qs or ss > qe) : 
        return 0; 

 # If a part of this segment overlaps 
    # with the given range 
  mid = getMid(ss, se); 
    
  return getSumUtil(st, ss, mid, qs, qe, 2 * si + 1) + \ 
      getSumUtil(st, mid + 1, se, qs, qe, 2 * si + 2); 

""" A recursive function to update the nodes 
which have the given index in their range. 
The following are parameters st, si, ss and se 
are same as getSumUtil() 
i --> index of the element to be updated. 
    This index is in the input array. 
diff --> Value to be added to all nodes 
which have i in range """
def updateValueUtil(st, ss, se, i, diff, si) : 

 # Base Case: If the input index lies 
    # outside the range of this segment 
 if (i < ss or i > se) : 
      return; 

   # If the input index is in range of this node, 
  # then update the value of the node and its children 
    st[si] = st[si] + diff; 
  
  if (se != ss) : 
 
      mid = getMid(ss, se); 
        updateValueUtil(st, ss, mid, i, 
                      diff, 2 * si + 1); 
       updateValueUtil(st, mid + 1, se, i, 
                      diff, 2 * si + 2); 

# The function to update a value in input array 
# and segment tree. It uses updateValueUtil() 
# to update the value in segment tree 
def updateValue(arr, st, n, i, new_val) : 

    # Check for erroneous input index 
   if (i < 0 or i > n - 1) : 
        
      print("Invalid Input", end = ""); 
        return; 

   # Get the difference between 
    # new value and old value 
   diff = new_val - arr[i]; 

   # Update the value in array 
 arr[i] = new_val; 

  # Update the values of nodes in segment tree 
    updateValueUtil(st, 0, n - 1, i, diff, 0); 

# Return sum of elements in range from 
# index qs (quey start) to qe (query end). 
# It mainly uses getSumUtil() 
def getSum(st, n, qs, qe) : 

  # Check for erroneous input values 
  if (qs < 0 or qe > n - 1 or qs > qe) : 

     print("Invalid Input", end = ""); 
        return -1; 
  
  return getSumUtil(st, 0, n - 1, qs, qe, 0); 

# A recursive function that constructs 
# Segment Tree for array[ss..se]. 
# si is index of current node in segment tree st 
def constructSTUtil(arr, ss, se, st, si) : 

   # If there is one element in array, 
 # store it in current node of 
   # segment tree and return 
   if (ss == se) : 
 
      st[si] = arr[ss]; 
        return arr[ss]; 
 
  # If there are more than one elements, 
  # then recur for left and right subtrees 
    # and store the sum of values in this node 
  mid = getMid(ss, se); 
    
  st[si] = constructSTUtil(arr, ss, mid, st, si * 2 + 1) +\ 
            constructSTUtil(arr, mid + 1, se, st, si * 2 + 2); 
   
  return st[si]; 

""" Function to construct segment tree 
from given array. This function allocates memory 
for segment tree and calls constructSTUtil() to 
fill the allocated memory """
def constructST(arr, n) : 

 # Allocate memory for the segment tree 

    # Height of segment tree 
    x = (int)(ceil(log2(n))); 

  # Maximum size of segment tree 
  max_size = 2 * (int)(2**x) - 1; 
  
  # Allocate memory 
   st = [0] * max_size; 

   # Fill the allocated memory st 
  constructSTUtil(arr, 0, n - 1, st, 0); 

 # Return the constructed segment tree 
   return st; 

# Driver Code 
if __name__ == "__main__" : 

    arr = [1, 3, 5, 7, 9, 11]; 
   n = len(arr); 

  # Build segment tree from given array 
   st = constructST(arr, n); 

  # Print sum of values in array from index 1 to 3 
    print("Sum of values in given range = ", 
                   getSum(st, n, 1, 3)); 

  # Update: set arr[1] = 10 and update 
    # corresponding segment tree nodes 
  updateValue(arr, st, n, 1, 10); 

    # Find sum after the value is updated 
   print("Updated sum of values in given range = ", 
                   getSum(st, n, 1, 3), end = "");

Output:

1 2	Sum of values in given range = 15 Updated sum of values in given range = 22

Time Complexity: Time Complexity for tree construction is O(n). There are total 2n-1 nodes, and value of every node is calculated only once in tree construction.

Time complexity to query is O(Logn). To query a sum, we process at most four nodes at every level and number of levels is O(Logn).

The time complexity of update is also O(Logn). To update a leaf value, we process one node at every level and number of levels is O(Logn).

示例题目

SPOJ-GSS1

You are given a sequence A[1], A[2], ..., A[N] . ( |A[i]| ≤ 15007 , 1 ≤ N ≤ 50000 ). A query is defined as follows: Query(x,y) = Max { a[i]+a[i+1]+...+a[j] ; x ≤ i ≤ j ≤ y }. Given M queries, your program must output the results of these queries.

Input
- The first line of the input file contains the integer N.
- In the second line, N numbers follow.
- The third line contains the integer M.
- M lines follow, where line i contains 2 numbers xi and yi.
Output

Your program should output the results of the M queries, one query per line.

Example
1
2
3
4
5
6
7
8
Input:
3
-1 2 3
1
1 2

Output:
2

大致翻译：给定一段长度为n的序列a1, a2, ..., an （a有正有负），每次询问[L, R] (即aL ~ aR)范围内的最大子段和，并涉及单点修改操作。

线段树：维护区间最大子段和。

这里不能用传统的线段树了，我们维护的值要更多。

定义：

线段树一共要维护4个值，如下：（每个值的含义都是相对于该结点对应区间[l, r]而言）

struct node
{
    int sum;       //[l,r]区间之和
    int max_sum;   //[l,r]内的最大子段和
    int max_pre;   //[l,r]内的最大前缀和
    int max_post;  //[l,r]内的最大后缀和
}t[maxn<<2];

向上传递

我们采用分治归并的思路，我们知道在l=r时这四个值都是确定的，都等于al。那么通过左右两边的四个值如何求出合并后的值呢。这里我觉得这段话讲的很清楚。

我们定义一个操作get(a, l, r)表示查询a序列[l, r]区间内的最大子段和。如何分治实现这个操作呢？对于一个区间l, r，我们取m = (l + r)/2，对区间[l,m] 和 [m+1, r]分治求解。当递归逐层深入直到区间长度缩小为1的时候，递归「开始回升」。这个时候我们考虑如何通过[l, m]区间的信息和[m+1, r]区间的信息合并成区间[l, r]的信息。最关键的两个问题是：

我们要维护区间的哪些信息呢？
我们如何合并这些信息？

对于一个区间[l, r]，我们可以维护四个量：

lSum表示[l, r]内以l为左端点的最大子段和
rSum表示[l, r]内以r为右端点的最大字段和
mSum表示[l, r]内的最大子段和
iSum表示[l, r]的区间和

以下简称[l, m]为[l, r]的「左子区间」，[m+1, r]为[l, r]的右子区间。我们考虑如何维护这些量呢（如何通过左右子区间的信息合并得到[l,r]的信息）？对于长度为1的区间[i,i]，四个量的值都和ai相等。对于长度大于1的区间：

首先最好维护的是iSum，区间[l, r]的iSum就等于「左子区间」的iSum加上「右子区间」的iSum。

对于[l, r]的lSum，存在两种可能，它要么等于「左子区间」的lSum，要么等于「左子区间」的iSum加上「右子区间」的lSum，两者取大。

对于[l, r]的rSum，同理，它要么等于「右子区间」的rSum，要么等于「右子区间」的iSum加上「左子区间」的rSum，两者取大。

当计算好上面的三个量之后，就很好计算[l, r]的mSum了。我们可以考虑[l, r]的mSum对应的区间是否跨越m--它可能不跨越m，也就是说[l, r]的mSum可能是「左子区间」的mSum和「右子区间」的mSum中的一个；它可能跨越m，可能是「左子区间」的rSum和「右子区间」的lSum求和。三者取大。

我们把这个过程叫做向上传递，英文叫做pushup。

如果我们把 [0,n−1] 分治下去出现的所有子区间的信息都用堆式存储的方式记忆化下来，即建成一颗真正的树之后，我们就可以在 O(logn) 的时间内求到任意区间内的答案，我们甚至可以修改序列中的值，做一些简单的维护，之后仍然可以在 O(logn) 的时间内求到任意区间内的答案，对于大规模查询的情况下，这种方法的优势便体现了出来。这棵树就是线段树。

leetcode，53. 最大子序和，可用dp也可用线段树求解。与上一题一样，只不过上一题有多个query，适合把线段树存下来。

示例解法：

# 线段树
# 我们定义一个操作get(a, l, r)表示查询a序列[l, r]区间内的最大子段和，
# 那么最终我们要求的答案就是get(arr, 0, n-1)。如何分治实现这个操作呢？
# 对于一个区间l, r，我们取m = (l + r)/2， 对区间[l,m] 和 [m+1, r]分治求解。
# 当递归逐层深入直到区间长度缩小为1的时候，递归「开始回升」。
# 这个时候我们考虑如何通过[l, m]区间的信息和[m+1, r]区间的信息合并成区间[l, r]的信息。
# 最关键的两个问题是：
# 我们要维护区间的哪些信息呢？
# 我们如何合并这些信息？
# 对于一个区间[l, r]，我们可以维护四个量：
# lSum表示[l, r]内以l为左端点的最大子段和
# rSum表示[l, r]内以r为右端点的最大字段和
# mSum表示[l, r]内的最大子段和
# iSum表示[l, r]的区间和
# 以下简称[l, m]为[l, r]的「左子区间」，[m+1, r]为[l, r]的右子区间。
# 我们考虑如何维护这些量呢（如何通过左右子区间的信息合并得到[l,r]的信息）？
# 对于长度为1的区间[start,start]，四个量的值都和ai相等。对于长度大于1的区间：
# 首先最好维护的是iSum，区间[l, r]的iSum就等于「左子区间」的iSum加上「右子区间」的iSum。
# 对于[l, r]的lSum，存在两种可能，它要么等于「左子区间」的lSum，
# 要么等于「左子区间」的iSum加上「右子区间」的lSum，两者取大。
# 对于[l, r]的rSum，同理，它要么等于「右子区间」的rSum，
# 要么等于「右子区间」的iSum加上「左子区间」的rSum，两者取大
# 当计算好上面的三个量之后，就很好计算[l, r]的mSum了。
# 我们可以考虑[l, r]的mSum对应的区间是否跨越m--它可能不跨越m，
# 也就是说[l, r]的mSum可能是「左子区间」的mSum和「右子区间」
# 的mSum中的一个；
# 它可能跨越m，可能是「左子区间」的rSum和「右子区间」的lSum求和。三者取大。
# 时间复杂度，相当于遍历一个二叉树的所有结点，结点最多为2*n个，所以时间为O(n)
# 空间复杂度：递归：O(logn)
class Solution:
    def maxSubArray(self, nums: List[int]) -> int:
        l, r = 0, len(nums) - 1
        return self.get(nums, l, r)[2]

    def get(self, nums, l, r):
        if l == r:
            return [nums[l]] * 4

        mid = l + ((r - l) >> 1)
        lSum1, rSum1, mSum1, iSum1 = self.get(nums, l, mid)
        lSum2, rSum2, mSum2, iSum2 = self.get(nums, mid + 1, r)
        iSum = iSum1 + iSum2
        lSum = max(lSum1, iSum1 + lSum2)
        rSum = max(rSum2, iSum2 + rSum1)
        mSum = max(mSum1, mSum2, rSum1 + lSum2)
        return lSum, rSum, mSum, iSum


# 存储一颗线段树
class Solution:
    def maxSubArray(self, nums: List[int]) -> int:
        l, r = 0, len(nums) - 1
        memo = {}
        res = self.build(nums, l, r, memo)[2]
        print(memo)
        return res

    def build(self, nums, l, r, memo):
        if l == r:
            memo[l, r] = [nums[l]] * 4
            return [nums[l]] * 4

        mid = l + ((r - l) >> 1)
        lSum1, rSum1, mSum1, iSum1 = self.build(nums, l, mid, memo)
        lSum2, rSum2, mSum2, iSum2 = self.build(nums, mid + 1, r, memo)
        iSum = iSum1 + iSum2
        lSum = max(lSum1, iSum1 + lSum2)
        rSum = max(rSum2, iSum2 + rSum1)
        mSum = max(mSum1, mSum2, rSum1 + lSum2)
        memo[l, r] = [lSum, rSum, mSum, iSum]
        return lSum, rSum, mSum, iSum


# f(i) s[:i]的最大子序和，且一定包括i
# f(i) = max(f(i-1), 0) + a[i]
class Solution:
    def maxSubArray(self, nums: List[int]) -> int:
        pre, cur = float('-inf'), float('-inf')
        for n in nums:
            pre = max(pre + n, n)
            cur = max(cur, pre)
        return cur


# 「方法二」相较于「方法一」来说，时间复杂度相同，但是因为使用了递归，并且维护了四个信息的结构体，
# 运行的时间略长，空间复杂度也不如方法一优秀，而且难以理解。
# 那么这种方法存在的意义是什么呢？
#
# 对于这道题而言，确实是如此的。但是仔细观察「方法二」，它不仅可以解决区间 [0,n−1]，
# 还可以用于解决任意的子区间 [l,r] 的问题。
# 如果我们把 [0,n−1] 分治下去出现的所有子区间的信息都用堆式存储的方式记忆化下来，
# 即建成一颗真正的树之后，我们就可以在 O(logn) 的时间内求到任意区间内的答案，
# 我们甚至可以修改序列中的值，做一些简单的维护，
# 之后仍然可以在 O(logn) 的时间内求到任意区间内的答案，
# 对于大规模查询的情况下，这种方法的优势便体现了出来。
# 这棵树就是上文提及的一种神奇的数据结构——线段树。

参考：

实际问题（简单记，想快速知道数组的某一区间和，同时数组的修改频繁，使得这两种操作都变成O(logn)，用线段树，可利用思想解决最大子段和问题）

示例题目

SPOJ-GSS1

Input

Output

Example