侯瑞哲的博客

Ruizhe's Blog

0%

树状数组Binary Indexed Tree

发表于 更新于 Valine：

参考

https://www.geeksforgeeks.org/binary-indexed-tree-or-fenwick-tree-2/

实际问题（简单记，想快速知道数组的前缀和，同时数组的修改频繁，用树状数组，使得这两种操作都变成O(logn)，两边查询的树状数组可以相当于线段树的功能）

We have an array arr[0 . . . n-1]. We would like to 1 Compute the sum of the first i elements. 2 Modify the value of a specified element of the array arr[i] = x where 0 <= i <= n-1.

A simple solution is to run a loop from 0 to i-1 and calculate the sum of the elements. To update a value, simply do arr[i] = x. The first operation takes O(n) time and the second operation takes O(1) time.

Another simple solution is to create an extra array and store the sum of the first i-th elements at the i-th index in this new array. The sum of a given range can now be calculated in O(1) time, but the update operation takes O(n) time now. This works well if there are a large number of query operations but a very few number of update operations.

Could we perform both the query and update operations in O(log n) time? One efficient solution is to use Segment Tree that performs both operations in O(Logn) time.

An alternative solution is Binary Indexed Tree, which also achieves O(Logn) time complexity for both operations. Compared with Segment Tree, Binary Indexed Tree requires less space and is easier to implement..

给定一个数组[0, .., n-1]，我们想：

  1. 计算出前i个元素的和
  2. 将任何一个元素改为x，arr[i] = x where 0<=i<=n-1

和线段树的实际问题的区别在于，线段树是从l到r任何一段，树状数组只是前i个。

同样第一个简单的解法就是循环求和O(n)，改变为O(1)。

或者创建一个新数组的每个元素存的前i个数的和，这样求和就是O(1)，但是改变后数组就要调整O(n)的时间复杂度。

Representation Binary Indexed Tree is represented as an array. Let the array be BITree[]. Each node of the Binary Indexed Tree stores the sum of some elements of the input array. The size of the Binary Indexed Tree is equal to the size of the input array, denoted as n. In the code below, we use a size of n+1 for ease of implementation.

Construction We initialize all the values in BITree[] as 0. Then we call update() for all the indexes, the update() operation is discussed below.

Operations

1
2
3
4
5
6
7
8
getSum(x): Returns the sum of the sub-array arr[0,...,x]
// Returns the sum of the sub-array arr[0,...,x] using BITree[0..n], which is constructed from arr[0..n-1]
1) Initialize the output sum as 0, the current index as x+1.
2) Do following while the current index is greater than 0.
...a) Add BITree[index] to sum
...b) Go to the parent of BITree[index].  The parent can be obtained by removing
     the last set bit from the current index, i.e., index = index - (index & (-index))【index&(index-1) 也可以】
3) Return sum.

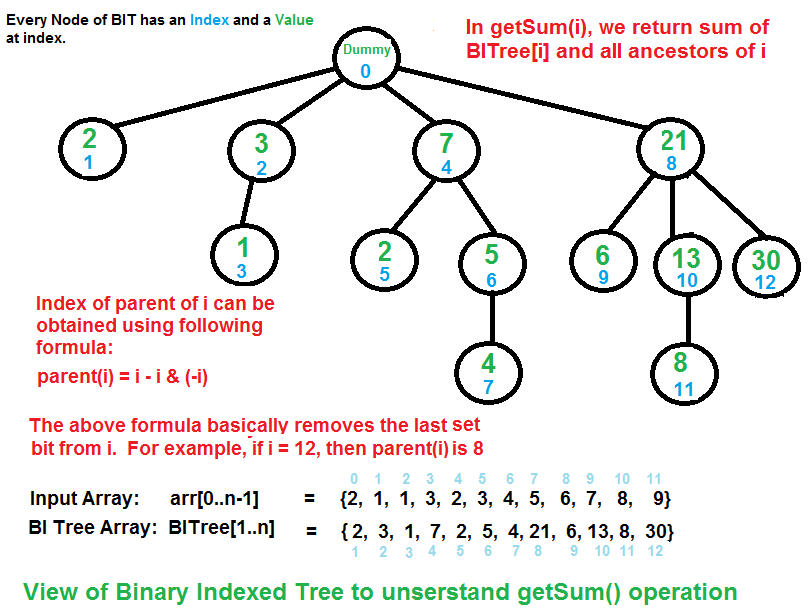
The diagram above provides an example of how getSum() is working. Here are some important observations.

BITree[0] is a dummy node.

BITree[y] is the parent of BITree[x], if and only if y can be obtained by removing the last set bit from the binary representation of x, that is y = x – (x & (-x)).【index&(index-1) 也可以】

The child node BITree[x] of the node BITree[y] stores the sum of the elements between y(inclusive) and x(exclusive): arr[y,…,x).

1
2
3
4
5
6
7
update(x, val): Updates the Binary Indexed Tree (BIT) by performing arr[index] += val
// Note that the update(x, val) operation will not change arr[].  It only makes changes to BITree[]
1) Initialize the current index as x+1.
2) Do the following while the current index is smaller than or equal to n.
...a) Add the val to BITree[index]
...b) Go to parent of BITree[index].  The parent can be obtained by incrementing
     the last set bit of the current index, i.e., index = index + (index & (-index))

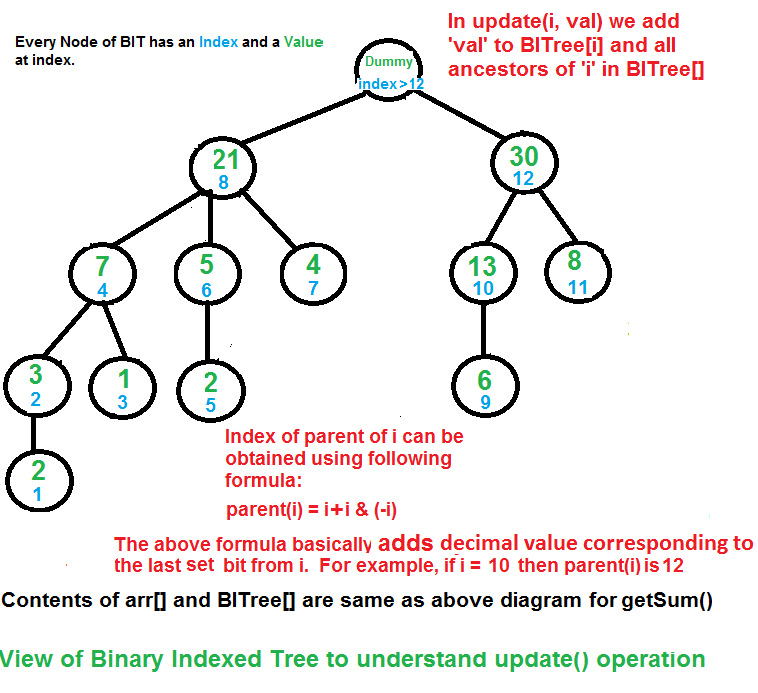
The update function needs to make sure that all the BITree nodes which contain arr[i] within their ranges being updated. We loop over such nodes in the BITree by repeatedly adding the decimal number corresponding to the last set bit of the current index.

How does Binary Indexed Tree work? The idea is based on the fact that all positive integers can be represented as the sum of powers of 2. For example 19 can be represented as 16 + 2 + 1. Every node of the BITree stores the sum of n elements where n is a power of 2. For example, in the first diagram above (the diagram for getSum()), the sum of the first 12 elements can be obtained by the sum of the last 4 elements (from 9 to 12) plus the sum of 8 elements (from 1 to 8). The number of set bits in the binary representation of a number n is O(Logn). Therefore, we traverse at-most O(Logn) nodes in both getSum() and update() operations. The time complexity of the construction is O(nLogn) as it calls update() for all n elements.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
# 树状数组binary-indexed-tree.py


class BITree:
    def __init__(self, nums):
        self.n = len(nums)
        self.tree = [0] * (self.n + 1)
        for i, num in enumerate(nums):
            self.update(i + 1, num)

    def update(self, i, k):
        """

        Args:
            i: 指的是更新数组中的第几个数，对应索引是i-1
            k: 更新的数值

        """
        while i <= self.n:
            self.tree[i] += k
            i += (i & -i)

    def getSum(self, i):
        """

        Args:
            i: 返回前几个数的前缀和

        Returns: 前i个数的前缀和

        """
        s = 0
        while i:
            s += self.tree[i]
            i -= (i & -i)
        return s


def main():
    nums = [1, 2, 3, 4]
    tree = BITree(nums)
    # 打印前1,2,3,4个数的前缀和
    print(tree.getSum(1))
    print(tree.getSum(2))
    print(tree.getSum(3))
    print(tree.getSum(4))
    # 更新第2个数的值，增加3
    tree.update(2, 3)
    # 再次打印前1,2,3,4个数的前缀和
    print(tree.getSum(1))
    print(tree.getSum(2))
    print(tree.getSum(3))
    print(tree.getSum(4))
    # 更新第2个数的值，减少3
    tree.update(2, -3)
    print(tree.getSum(1))
    print(tree.getSum(2))
    print(tree.getSum(3))
    print(tree.getSum(4))


if __name__ == '__main__':
    main()

Output:

1
2
Sum of elements in arr[0..5] is 12
Sum of elements in arr[0..5] after update is 18

Can we extend the Binary Indexed Tree to computing the sum of a range in O(Logn) time? Yes. rangeSum(l, r) = getSum(r) – getSum(l-1).

Applications: The implementation of the arithmetic coding algorithm.

典型题目

leetcode 315 计算右侧小于当前元素的个数

给定一个整数数组 nums，按要求返回一个新数组 counts。数组 counts 有该性质： counts[i] 的值是 nums[i] 右侧小于 nums[i] 的元素的数量。

示例：

输入：[5,2,6,1] 输出：[2,1,1,0] 解释： 5 的右侧有 2 个更小的元素 (2 和 1) 2 的右侧仅有 1 个更小的元素 (1) 6 的右侧有 1 个更小的元素 (1) 1 的右侧有 0 个更小的元素

链接：https://leetcode-cn.com/problems/count-of-smaller-numbers-after-self

树状数组解法，用每个数的rank来离散化，反序插入树状数组中，前一位的前缀和就是右侧小于当前元素的个数。

示例代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution:
    def countSmaller(self, nums: List[int]) -> List[int]:
        rank = {val: i + 1 for i, val in enumerate(sorted(nums))}
        n = len(nums)
        res = []

        BITree = [0] * (n + 1)

        def update(i, k=1):
            while i <= n:
                BITree[i] += k
                i += i & -i

        def getSum(i):
            s = 0
            while i:
                s += BITree[i]
                i -= i & -i
            return s

        for num in reversed(nums):
            res.append(getSum(rank[num] - 1))
            update(rank[num])

        return res[::-1]