侯瑞哲的博客

Ruizhe's Blog

0%

区间树

发表于 更新于 Valine：

参考：

https://www.geeksforgeeks.org/interval-tree/

https://stackoverflow.com/questions/17466218/what-are-the-differences-between-segment-trees-interval-trees-binary-indexed-t#:~:text=Segment%20tree%20stores%20intervals%2C%20and,with%20a%20given%20interval%22%20queries.

实际问题（简单记，类似于点的添加和删除和查找，都要快速，点的解决办法是平衡BST，使得这几种操作都变成O(logn)，区间的添加删除类似，查找的是overlap，这时就需要用到区间树）

Consider a situation where we have a set of intervals and we need following operations to be implemented efficiently. 1) Add an interval 2) Remove an interval 3) Given an interval x, find if x overlaps with any of the existing intervals.

考虑我们有一个集合的区间，并且我们需要以下操作能够有效率的实现：

  1. 添加一个区间
  2. 删除一个区间
  3. 对于一个给定的区间x，找出x是否有和任意一个已经存在的区间有重合。

Interval Tree: The idea is to augment a self-balancing Binary Search Tree (BST) like Red Black Tree, AVL Tree, etc to maintain set of intervals so that all operations can be done in O(Logn) time.

Every node of Interval Tree stores following information. a) i: An interval which is represented as a pair [low, high] b) max: Maximum high value in subtree rooted with this node.

区间的最小值用作BST的键值来保持BST的顺序。那么插入和删除就和自平衡BST的插入删除一样。

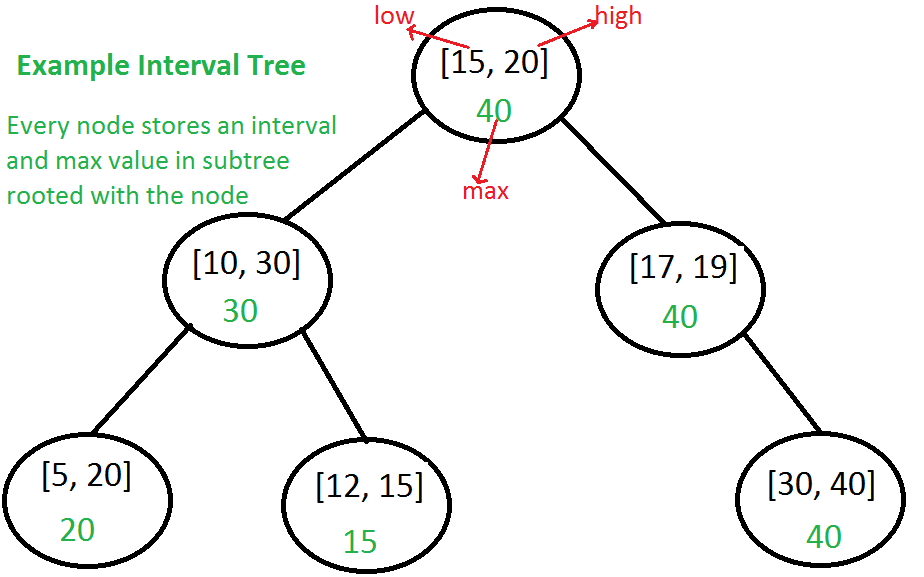
那么我们就来看找重合区间的操作。

Following is algorithm for searching an overlapping interval x in an Interval tree rooted with root.

1
2
3
4
5
6
7
Interval overlappingIntervalSearch(root, x)
1) If x overlaps with root's interval, return the root's interval.

2) If left child of root is not empty and the max  in left child 
is greater than x's low value, recur for left child

3) Else recur for right child.

How does the above algorithm work? Let the interval to be searched be x. We need to prove this in for following two cases.

Case 1: When we go to right subtree, one of the following must be true. a) There is an overlap in right subtree: This is fine as we need to return one overlapping interval. b) There is no overlap in either subtree: We go to right subtree only when either left is NULL or maximum value in left is smaller than x.low. So the interval cannot be present in left subtree.

Case 2: When we go to left subtree, one of the following must be true. a) There is an overlap in left subtree: This is fine as we need to return one overlapping interval. b) There is no overlap in either subtree: This is the most important part. We need to consider following facts. … We went to left subtree because x.low <= max in left subtree …. max in left subtree is a high of one of the intervals let us say [a, max] in left subtree. …. Since x doesn’t overlap with any node in left subtree x.low must be smaller than ‘a‘. …. All nodes in BST are ordered by low value, so all nodes in right subtree must have low value greater than ‘a‘. …. From above two facts, we can say all intervals in right subtree have low value greater than x.low. So x cannot overlap with any interval in right subtree.

Applications of Interval Tree: Interval tree is mainly a geometric data structure and often used for windowing queries, for instance, to find all roads on a computerized map inside a rectangular viewport, or to find all visible elements inside a three-dimensional scene (Source Wiki).

Interval Tree vs Segment Tree Both segment and interval trees store intervals. Segment tree is mainly optimized for queries for a given point, and interval trees are mainly optimized for overlapping queries for a given interval.

区间树和线段树都是存储区间的，不同的是线段是针对给定点的查询进行优化，区间树针对给定区间的重叠查询进行优化。