位运算解决全部其余所有数出现k次，找出唯一出现p次的数的题目

1. 问题描述

给出只包含int类型的数组，所有值出现k(k>1)次，除了一个值，这个值出现了p次（p>1, p%k!=0)。找到这个值。

2. 从只有1bit的特殊情况开始

为了应用位运算，我们应该重新思考integers是如何在计算机中被表示的--通过位。让我们先考虑1位。假如我们有一数组的一bit数（除了0就是1），我们要统计数组中的1，使得当统计1的计数器到达k时，计数器回到0并且重新统计（k和我们问题中提到的k一样）。为了跟踪我们已经遇到多少个1，我们需要一个计数器。假设计数器二进制表示有m位：xm, ..., x1（最重要的位到最不重要的位）。我们至少可以总结出计数器的以下四个特性。

计数器有一个初始状态，简单来讲为0
对于数组中的每一个输入，如果我们击中0，计数器应该保持不变
对于数组中的每一个输入，如果我们击中1，计数器应该增加1
为了覆盖k个计数，我们要求2^m>=k，这意味着m > logk

这里是关键部分：当我们扫描数组时，计数器（从x1到xm）中的每个位如何变化。注意，我们被提示使用位运算。为了满足第2个属性，回想一下，如果另一个操作数为0，有哪些位操作不会改变操作数？是的，有位与x=x|0和位异或x=x^0。

好了，我们现在有一个表达式：x = x | i或者x = x^i，其中i是数组中的扫描元素。哪一个更好呢？我们还不知道。所以，让我们开始实际的计算。

开始的时候，计数器的所有位都初始化为0，即xm=0, ..., x1=0。由于我们要选择的位操作，保证了计数器的所有位在遇到0时都保持不变，所以直到我们遇到数组中第一个1，计数器将是0。当我们遇到第一个1的时候，我们得到：xm = 0, ... , x2=0, x1=1。让我们继续下去，直到打出第二个1，之后我们得到：xm=0, ... , x2=1, x1=0。注意，x1从1变成了0。对于x1 = x1 | i，在第二次计数之后，x1仍然会是1。所以很明显，我们应该使用x1 = x1 ^ i，那么x2, ..., xm呢？我们的想法是找到x2, ... , xm将改变其值的条件。以x2为例。如果我们打了一个1，需要改变x2的值，那么在我们进行改变之前，x1的值一定是多少？答案是：x1必须是1，否则我们不应该改变x2，因为把x1从0改成1就可以了。因此，只有当x1和i都是1时，x2才会改变值，或者数学上说，x2 = x2 ^ (x1 & i)。同理，xm只有在，xm-1, ... , x1和i都是1的时候才会改变数值：xm = xm ^ (xm-1 & ... & x1 & i)。ok，我们找到了这个位运算。

但是，你可能会注意到，上面发现的位运算将从0开始计数，直到2^m-1，而不是k。如果k < 2^m - 1，我们需要一些”切割“机制，以在计数达到k时将计数器重新初始化为0。为此，我们对xm, ... , x1应用位AND，并使用一些称为mask的变量，即xm = xm & mask, ... , x1 = x1 & mask。如果我们能保证只有当计数达到k时，mask才为0，而在其他所有计数情况下为1，那么我们就完成了。我们如何实现这一点呢？试着想一想，计数为k的情况与其他所有情况的区别是什么？是的，是1的计数！对于每一个计数，我们对计数器的每一个位都有唯一的值，这可以看作是它的状态。如果我们把k写成二进制形式：km, ... ,k1, 我们就可以构造mask如下。

mask = ~(y1 & y2 & .. & ym)，其中如果kj = 1, yj = xj，如果kj = 0， yj = -xj ( j = 1 to m )

简单来讲，就是只有当x1..xm和k的所有位都相等的时候，mask才会为0

我们来举一些例子：

k = 3: k1 = 1, k2 = 1, mask = ~(x1 & x2);

k = 5: k1 = 1, k2 = 1, k3 = 1, mask = ~(x1 & ~x2 & x3);

综上所述，我们的算法将是这样的（nums是输入数组）：

for (int i : nums) {
    xm ^= (xm-1 & ... & x1 & i);
    xm-1 ^= (xm-2 & ... & x1 & i);
    .....
    x1 ^= i;
    
    mask = ~(y1 & y2 & ... & ym) where yj = xj if kj = 1, and yj = ~xj if kj = 0 (j = 1 to m).

    xm &= mask;
    ......
    x1 &= mask;
}

3. 32位数的一般情况

现在是时候把我们的结果从1位数的情况推广到32位整数了。一个直接的方法是为整数中的每个位创建32个计数器。但是，如果我们利用位操作的优势，我们也许可以”集体“管理所有的32个计数器，其中m是满足m>=logk的最小整数。原因是位操作只适用于每个位，所以对不同位的操作是相互独立的（有点明显，对吧？）。这使得我们可以将32个计数器的对应位归为一个32位整数。下面是一个示意图，展示了如何做到这一点。

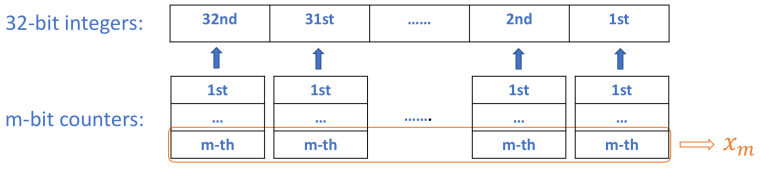
最上面的一行是32位的整数，其中每一个位，我们都有一个对应的m位计数器（由向上箭头下面的那一列所示）。由于对32位中每一个位的操作都是相互独立的，所以我们可以将比如说所有计数器的第m位，归为一个32位数（由橙色框所示）。这个32位数中的所有位（表示为xm）将遵循相同的位操作。由于每个计数器有m个位，我们最终得到m个32位数，对应于第二部分中定义的x1, ... , xm，但现在它们是32位数而不是1位数。因此，在上面开发的算法中，我们只需要将x1到xm视为32位整数而不是1位数。其他一切都将是相同的，我们就完成了。很简单，嗯？

4. 返回什么

最后就是我们应该返回什么值，或者等价于x1到xm中哪一个会等于单一元素。为了得到正确的答案，我们需要了解m个32位整数x1到xm代表什么。以x1为例，x1有32位，我们把它们标注为r（r=1到32)。当我们扫描完输入数组后，x1的r-th位的值将由数组中所有元素的r-th为决定（更具体的说，假设数组中所有元素的r-th位1的总计数为q，那么最终r-th位就是q'=q%k，其二进制形式为：q'm, ... , q'1，那么根据定义，x1的r-th位将等于 q'1)。现在你可以问自己这个问题：如果x1的r-th位是1，这意味着什么？

答案是要找到能对这个1做出贡献的东西，一个出现了k次的元素会有贡献吗？不会，为什么？因为一个元素要做出贡献，至少要同时满足两个条件：这个元素的r-th位是1，这个1的出现次数不是k的整数倍，第一个条件是微不足道的。第二个条件来自于每当1的命中次数为k时，计数器就会回零，也就是x1中的对应位会被重置为0，对于一个出现了k次的元素，不可能同时满足这两个条件（违反第二条），所以它不会有贡献。所以，只有出现p（p%k!=0）次的单个元素才会做出贡献。如果p>k，那么前k*[p/k] ([p/k]表示p/k的整数部分)的元素也不会做出贡献。所以我们总是可以设置p' = p % k，并说这个单元素有效地出现了p'次。

我们把p‘写成二进制形式：p'm, ... , p'1(注意p' < k, 所以它将适合m位)。这里提出一个声明，xj等于这个单个元素的条件是p'j = 1(j =1 到 m)，下面给出一个快速证明：

如果xj的r-th位是1，我们可以放心的说这个单一元素的r-th位也是1（否则没有任何东西可以使xj的r-th位是1）。我们还要证明，如果xj的r-th位是0，那么单元素的r-th位只能是0，我们就假设在这种情况下，单元素的r-th位是1，我们看看会发生什么。在扫描结束时，这个1将被计算p'次。根据定义，xj的r-th位将等于p'j，也就是1，这与xj的r-th位为0的假设相矛盾，因此我们得出结论，只要p'j=1，xj的r-th位将始终与单一元素的r-th位相同。由于这对xj中的所有位都是真的（即对若r=1到32来说是真的），所以我们得出结论，只要p'j=1，xj将等于这个单一元素的值。

所以现在我们应该返回什么就很清楚了。只要用其二进制形式表达p'=p%k，只要p'j = 1，就可以返回对应的xj中的任何一个。总的来说，该算法将在O(n*logk)时间和O(logk)的空间内运行。

快速例子几个

Here is a list of few quick examples to show how the algorithm works (you can easily come up with other examples):

k = 2, p = 1 k is 2, then m = 1, we need only one 32-bit integer (x1) as the counter. And 2^m = k so we do not even need a mask! A complete java program will look like:

public int singleNumber(int[] nums) {
    int x1 = 0;
     
    for (int i : nums) {
        x1 ^= i;
    }
     
    return x1;
}

k = 3, p = 1 k is 3, then m = 2, we need two 32-bit integers(x2, x1) as the counter. And 2^m > k so we do need a mask. Write k in its binary form: k = '11', then k1 = 1, k2 = 1, so we have mask = ~(x1 & x2). A complete java program will look like:

public int singleNumber(int[] nums) {
    int x1 = 0, x2 = 0, mask = 0;
     
    for (int i : nums) {
        x2 ^= x1 & i;
        x1 ^= i;
        mask = ~(x1 & x2);
        x2 &= mask;
        x1 &= mask;
    }

    return x1;  // Since p = 1, in binary form p = '01', then p1 = 1, so we should return x1. 
                // If p = 2, in binary form p = '10', then p2 = 1, and we should return x2.
                // Or alternatively we can simply return (x1 | x2).
}

k = 5, p = 3 k is 5, then m = 3, we need three 32-bit integers(x3, x2, x1) as the counter. And 2^m > k so we need a mask. Write k in its binary form: k = '101', then k1 = 1, k2 = 0, k3 = 1, so we have mask = ~(x1 & ~x2 & x3). A complete java program will look like:

public int singleNumber(int[] nums) {
    int x1 = 0, x2 = 0, x3  = 0, mask = 0;
   
    for (int i : nums) {
        x3 ^= x2 & x1 & i;
        x2 ^= x1 & i;
        x1 ^= i;
        mask = ~(x1 & ~x2 & x3);
        x3 &= mask;
        x2 &= mask;
        x1 &= mask;
    }
    
    return x1;  // Since p = 3, in binary form p = '011', then p1 = p2 = 1, so we can return either x1 or x2. 
                // If p = 4, in binary form p = '100', only p3 = 1, which implies we can only return x3.
                // Or alternatively we can simply return (x1 | x2 | x3).
}

Lastly I would like to thank those for providing feedbacks to make this post better. Hope it helps and happy coding!

侯瑞哲的博客